Home
Class 12
PHYSICS
Obtain the maximum kinetic energy of bet...

Obtain the maximum kinetic energy of `beta`-particles, and the radiation frequencies of `gamma` decays in the decay scheme shown in Fig. `14.6`. You are given that `m(.^(198)Au)=197.968233 u, m(.^(198)Hg)=197.966760 u`

Text Solution

Verified by Experts

`gamma`-rays are elctro magnetic radiations having energy `E=h upsilonrArrupsilon=(E)/(h)` where `h=`plank's constant`=6.625xx10^(-34)J.S`
1) Frequencies of `gamma_(1),gamma_(2)` and `gamma_(3)` are calculated as follows
`gamma_(1)=(DeltaE)/(h)=((1.088-0)MeV)/(6.625xx10^(-34)J.s)`
`=(1.088xx10^(6)xx1.6xx10^(-19))/(6.625xx10^(-34))`
`0.2627xx10^(21)=2.627xx10^(20)Hz`
`gamma_(2)=(DeltaE)/(h)=((0.412-0)MeV)/(6.625xx10^(-34)Js)`
`=(0.412xx1.6xx10^(-19)xx10^(6))/(6.625xx10^(-34))`
`=0.0995xx10^(21)=9.95xx10^(19)Hz`
`gamma_(3)=(DeltaE)/(h)=((1.088-0.412)xx10^(6)xx1.6xx10^(-19))/(6.625xx10^(-34))`
`=0.1632xx10^(21)=1.62xx10^(20)Hz`
2) Now maximum `K.E` of `beta_(1)^(-)=[M(.^(198)._(79)Au)M(.^(198)._(80)Hg)-(1.088)/(931.5)]c^(2)`
`(because 1 amu = 931.5 MeV rArr1 MeV=(1)/(931.5)U)`
`=[197.968233-197.966760-0.00168]931.5MeV`
`=0.000305xx931.5=0.284 MeV`
Maximum `K.E` of `beta_(2)^(-)=`
`[M(.^(198)._(79)Au)-M(.^(198)._(80)Hg)-(0.412)/(931.5)]c^(2)`
`=[197.968233-197.966760-0.000442]931.5`
`=0.001031xx931.5=0.9603 MeV`
Promotional Banner

Topper's Solved these Questions

  • NUCLEAR PHYSICS

    NARAYNA|Exercise C.U.Q|191 Videos

  • NUCLEAR PHYSICS

    NARAYNA|Exercise Level-1 (C.W)|21 Videos

  • MOVING CHARGES AND MAGNETISM

    NARAYNA|Exercise EXERCISE - 4|20 Videos

  • NUCLEI

    NARAYNA|Exercise ASSERTION & REASON|5 Videos

Similar Questions

Explore conceptually related problems

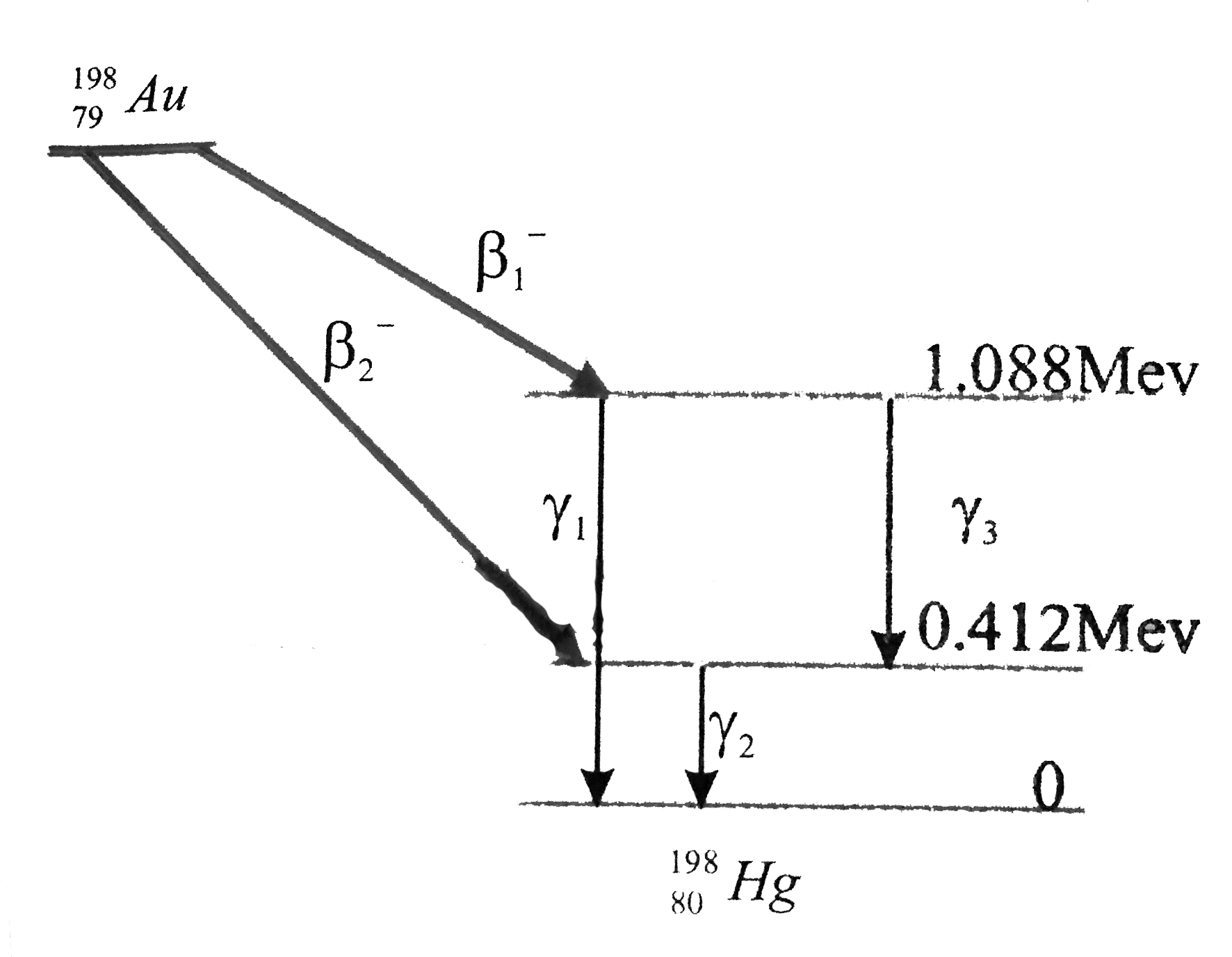
Calculate the kinetic energy of beta -particles and the radiation frequencies corresponding to the gamma -decays shown in figure. Given, mass of ._12Mg^27 atom =26.991425 amu and mass of ._13Al^27 atom = 26.990080 amu

Calculate the maximum kinetic energy of the bera particle emitted in the following decay scheme: ^12N rarr 12C **+e^(+)+v ^12C rarr ^12C + gamma(4.43 MeV). The atomic mass of 12N is 12.018612 u.

Calculate the maximum energy that a beta particle can have in the following decay: ._(8)O^(19) to ._(9)F^(19)+._(-1)e^(0)+barV Given, m(._(8)O^(19))=19.003576u, m(._(9)F^(19))=18.998403u, m(._(-1)e^(0))=0.000549u

Gold ._(79)^(198)Au undergoes beta^(-) decay to an excited state of ._(80)^(198)Hg . If the excited state decays by emission of a gamma -photon with energy 0.412 MeV , the maximum kinetic energy of the electron emitted in the decay is (This maximum occurs when the antineutrino has negligble energy. The recoil enregy of the ._(80)^(198)Hg nucleus can be ignored. The masses of the neutral atoms in their ground states are 197.968255 u for ._(79)^(198)Hg ).

A nucleus ""_(10)Ne^(23) undergoes beta - decay and becomes ""_(11)Na^(23) . Calculate the maximum kinetic energy of electrons emitted assuming that the daughter nucleus and antineutrino carry negligible kinetic energy. Given mass of ""_(10)Ne^(23) = 22.994466 u and mass of ""_(11)Na^(23) = 22.989770 m

Consider one of the fission reactions of U^(235) by thernmal neutrons : ._(92)U^(235) + n rarr ._(38)Sr^(94) + ._(54)Ce^(140) + 2n The fission fragments are, however, not stable. They unaergo successive beta- decays unit ._(38)Sr^(94) becomes ._(40)Zr^(94) and ._(54)Xe^(140) becomes ._(58)Ce^(140) . Estimate the total energy released in the process. Is all that energy available as kinetic energy of the fission products (Zr and Ce)? You are given that m (U^(235)) = 255.0439 am u," " m_(n) = 1.00866 am u " " m(Zr^(94)) = 93.9065 am u, " " m(Ce^(140)) = 139.9055 am u

Consider the beta decay ^198 Au rarr ^198 Hg ** + Beta^(-1) + vec v . where ^198 Hg^** represents a mercury nucleus in an excited state at energy 1.088 MeV above the ground state. What can be the maximum kinetic energy of the electron emitted? The atomic mass of ^198 Au is 197.968233 u and that of ^198 Hg is 197.966760 u .