Similar Questions
Explore conceptually related problems
Recommended Questions
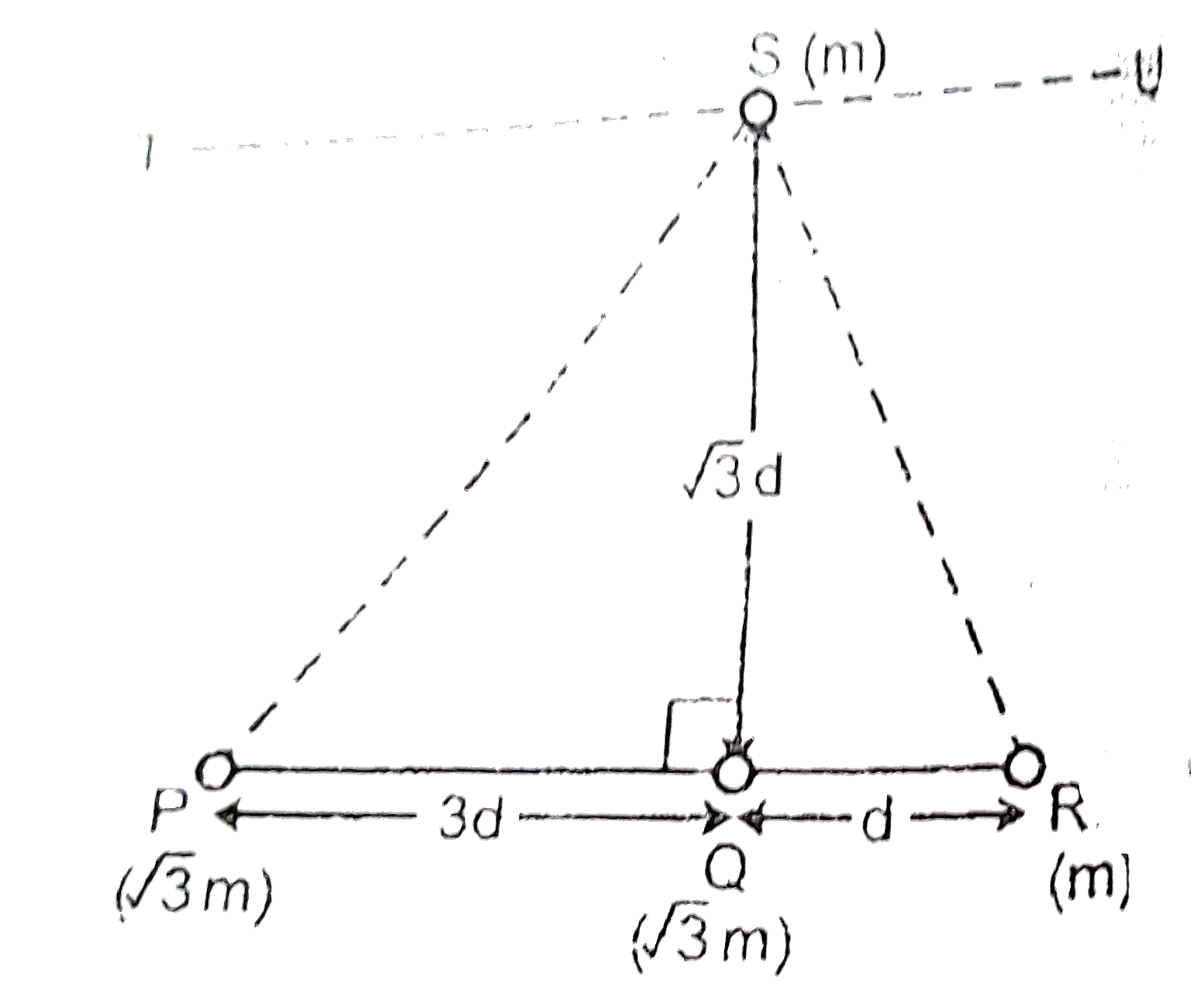
- Three particales P,Q and R are placedd as per given Masses of P,Q and ...
Text Solution
|
- If P = {a , b , c}and A xxB = {(p , q), (p , r), (m , q), (m , r)}Q = ...
Text Solution
|
- In Figure, /Q P R=/P Q R and M and N are respectively on sides Q...
Text Solution
|
- In Delta P Q R , if P Q=Q R and L ,M and N are the mid-points ...
Text Solution
|
- In P Q R , M and N are points on sides P Q and P R respectively ...
Text Solution
|
- In Fig. 4.238, S and T are points on the sides P Q and P R respe...
Text Solution
|
- Given P=0.0030 m, Q=2.40 m, R=3000 m, Significant figures in P, Q and ...
Text Solution
|
- In a scale of 10^(-18)m, match the particle with respect to their prob...
Text Solution
|
- Three particales P,Q and R are placedd as per given Masses of P,Q and ...
Text Solution
|
 .
.