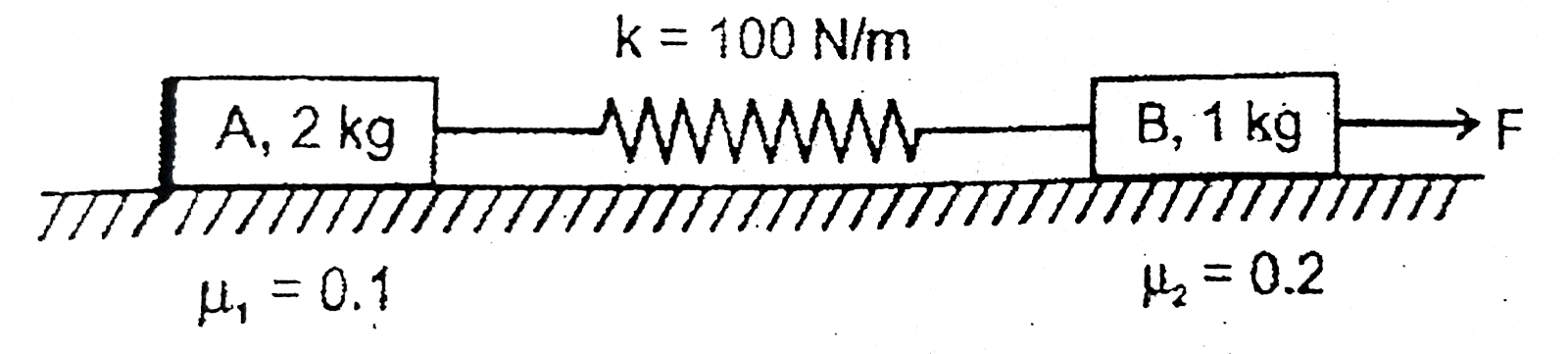Similar Questions
Explore conceptually related problems
Recommended Questions
- Initialy spring is in the natural length and blocks A & B are at rest....
Text Solution
|
- Initialy spring is in the natural length and blocks A & B are at rest....
Text Solution
|
- Block A of mass m is placed on a plank B . A light support S is fixed ...
Text Solution
|
- A block of mass m = 2 kg is connected to a a spring of force constant ...
Text Solution
|
- A block of mass m = 2 kg is connected to a spring of force constant k ...
Text Solution
|
- A block of mass 5 kg is released from rest when compression in spring ...
Text Solution
|
- चित्र में दो गुटके दिखाए गए हैं जिनके द्रव्यमान m तथा M है। ये गुटके ए...
Text Solution
|
- Force constant of a spring is 100 N//m . If a 10kg block attached with...
Text Solution
|
- Two blocks are connected by a spring of natural length 2 m. The force ...
Text Solution
|