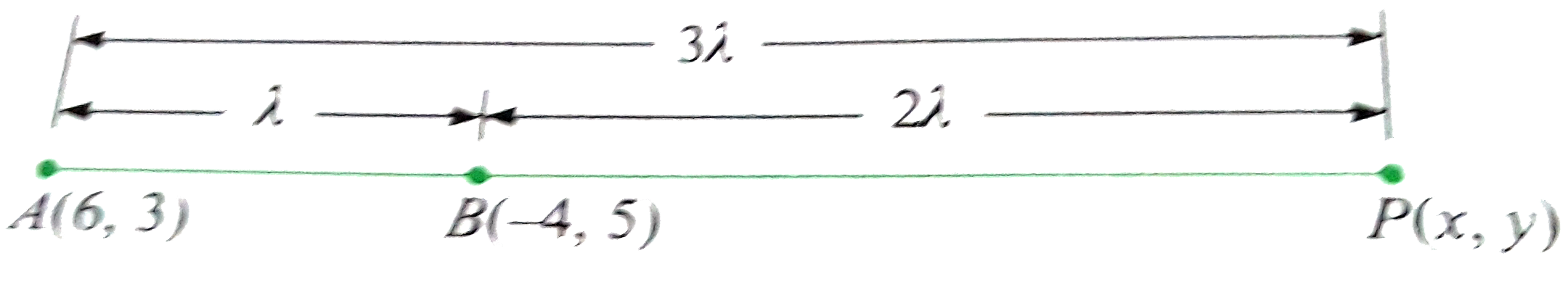Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- (i) Find the coordinates of the point which divides the line segment j...
Text Solution
|
- Find the coordinates of the point which divides the line segment join...
Text Solution
|
- Find the coordinates of the point which divides the line segment join...
Text Solution
|
- Internal division + proof + example :-Find the coordinates of a point ...
Text Solution
|
- external division + proof + example:-Find the coordinates of a point w...
Text Solution
|
- Find the coordinates of the point which divides the line segment j...
Text Solution
|
- Find the coordinates of the point which divides the line segment joini...
Text Solution
|
- Find the coordinates of the point which divides the line segment joini...
Text Solution
|
- Find the coordinates of the point which divides the line segment joini...
Text Solution
|