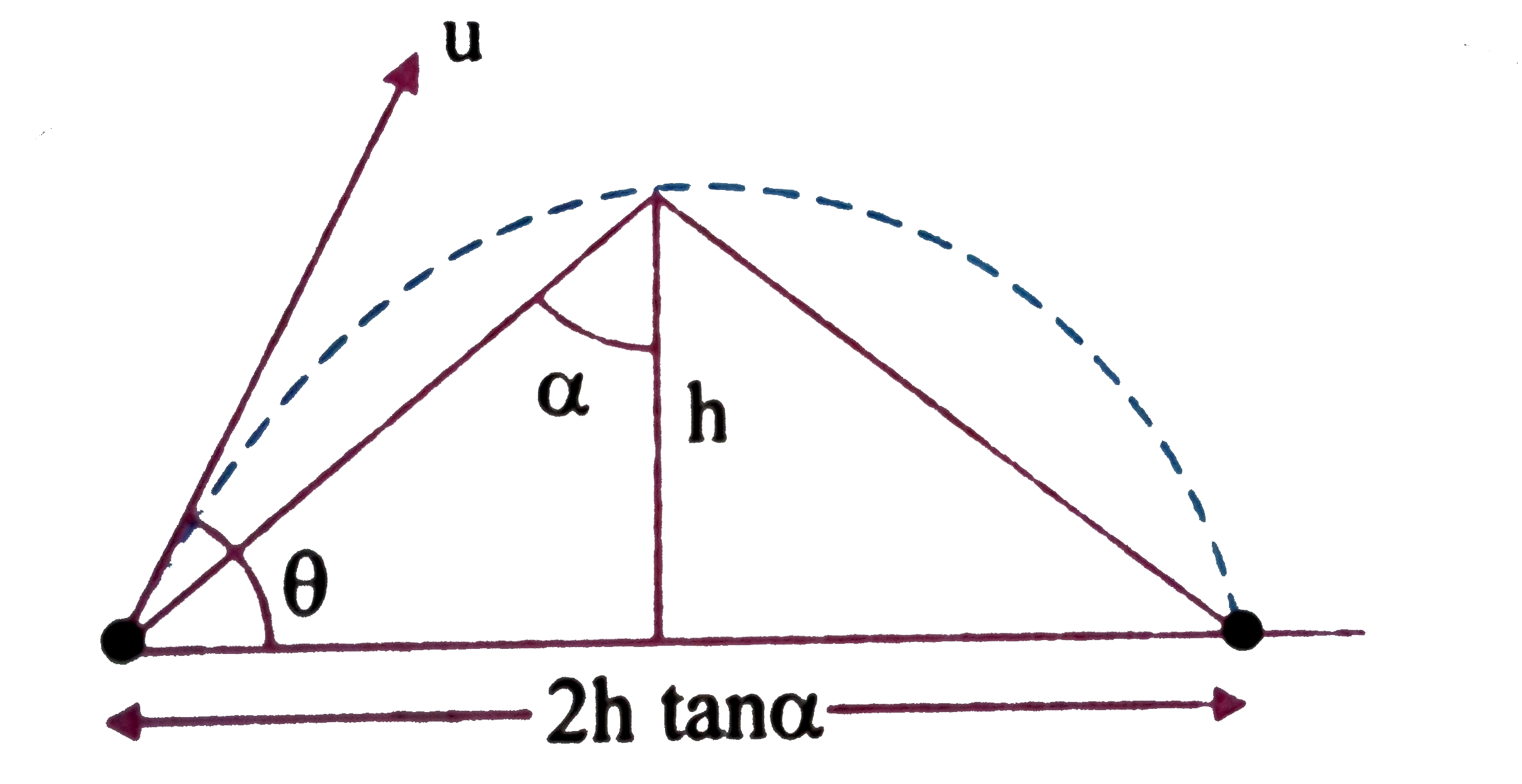
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MOTION IN A PLANE
NARAYNA|Exercise Level-Vi single answer|30 VideosMOTION IN A PLANE
NARAYNA|Exercise Level-Vi multiple answer|16 VideosMOTION IN A PLANE
NARAYNA|Exercise Level -V Passage|15 VideosMECHANICAL PROPERTIES OF SOLIDS
NARAYNA|Exercise LEVEL-II (H.W)|24 VideosMOTION IN A STRAIGHT LINE
NARAYNA|Exercise Level 2 H.W|29 Videos
Similar Questions
Explore conceptually related problems
NARAYNA-MOTION IN A PLANE-Integer
- Three points are located at the vertices of an equilateral triangle ea...
Text Solution
|
- The slopes of wind screen of two cars are alpha1=30^@ and alpha2= 15^@...
Text Solution
|
- A heavy particles is projected from a point at the foot of a fixed pla...
Text Solution
|
- A projectile is fired from the base of coneshaped hill. The projectil...
Text Solution
|
- Three balls A,B and C are projected from ground with same speed at sam...
Text Solution
|
- In figure, the angle of inclination of the inclined plane is 30^@. Fin...
Text Solution
|