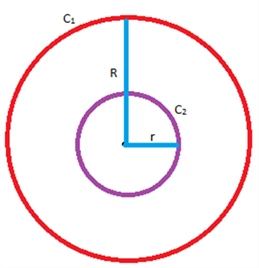
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Similar Triangles and their properties
Text Solution
|
- Similar Triangles and their properties
Text Solution
|
- The similarity in the properties of alkali metlas is due to
Text Solution
|
- State the two properties which are encessary for given two triangle to...
Text Solution
|
- IF one angle of a triangle is equal to one angle of another triangle a...
Text Solution
|
- Chemical properties of the members of a are similar.
Text Solution
|
- Introduction | Similar Figures | Similar Triangle And Congruent Triang...
Text Solution
|
- సరూప త్రిభుజాముల ధర్మముల రెండింటిని వ్రాయుము.
Text Solution
|
- The properties of Zr and Hf are similar because :
Text Solution
|