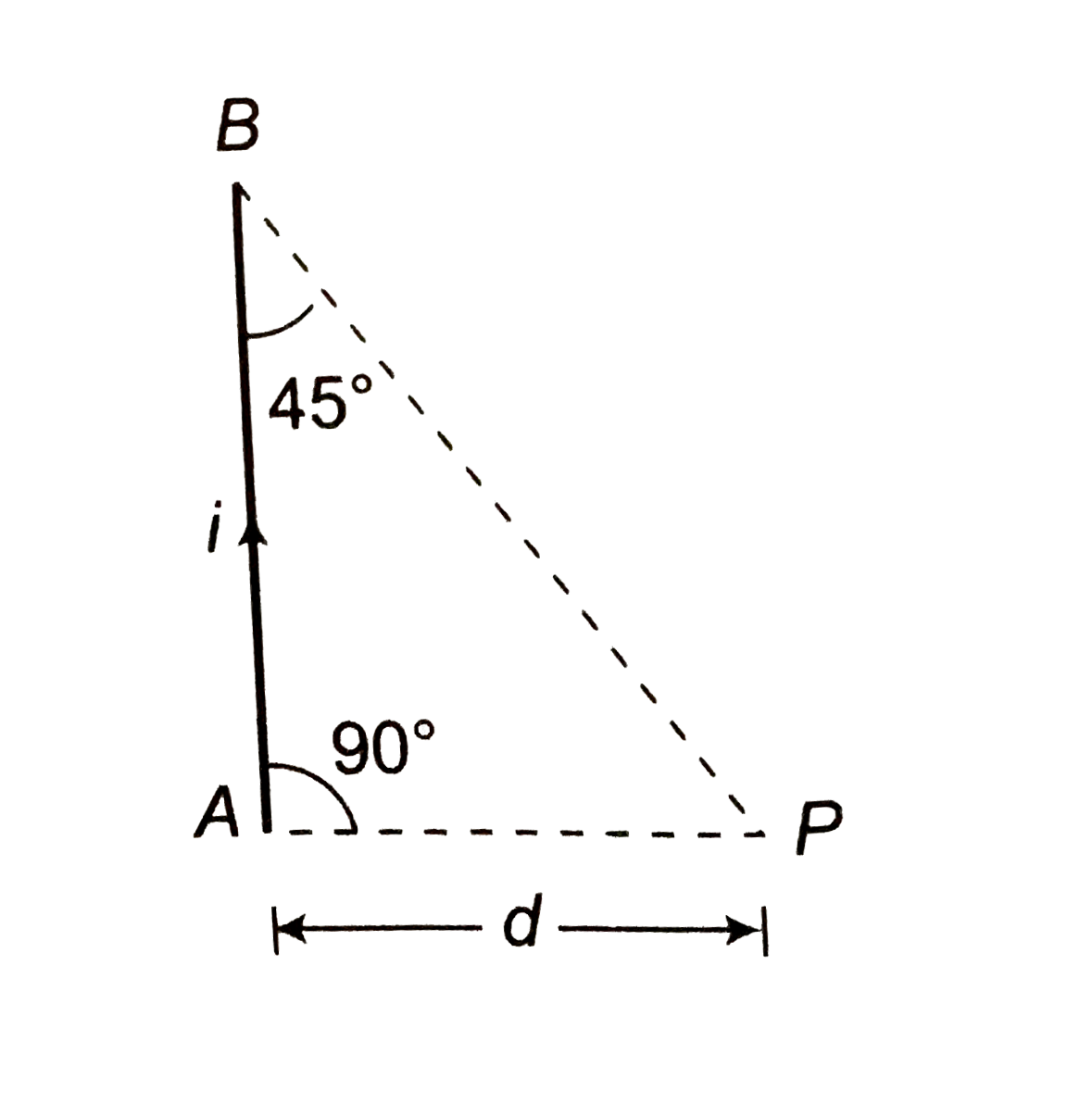Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CP SINGH-MAGNETIC FIELD-EXERCISE
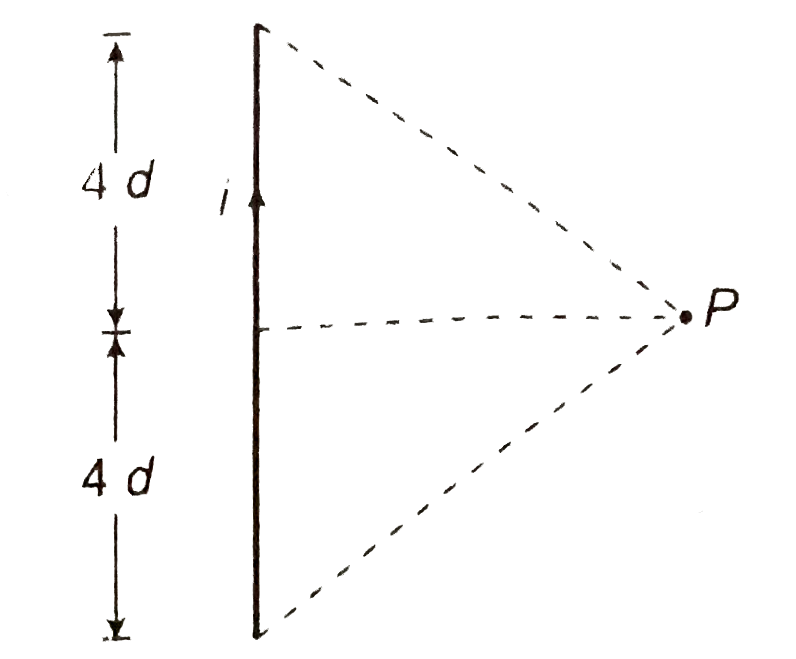
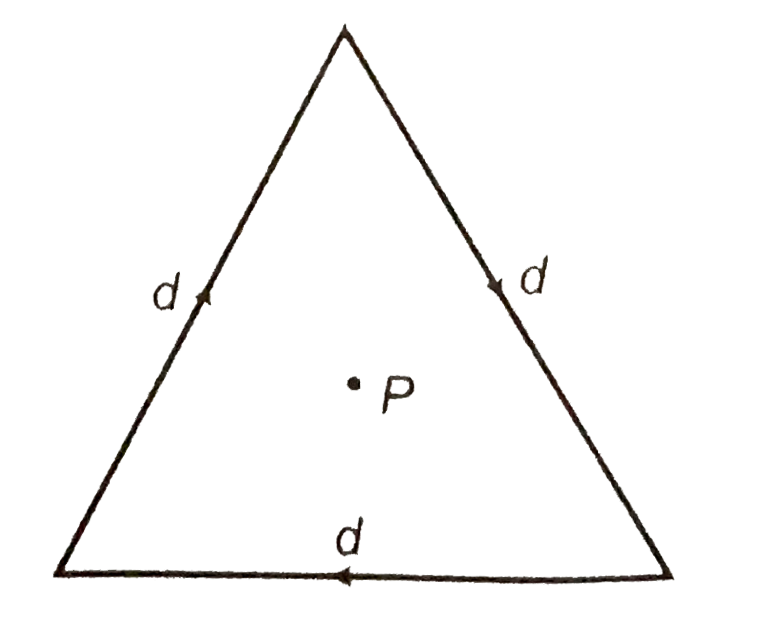
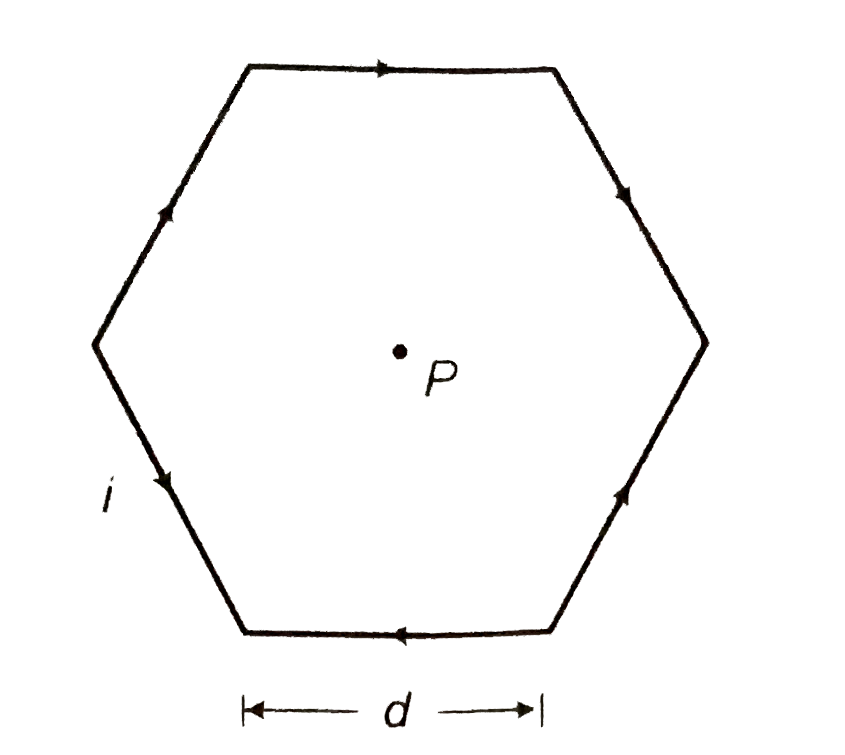
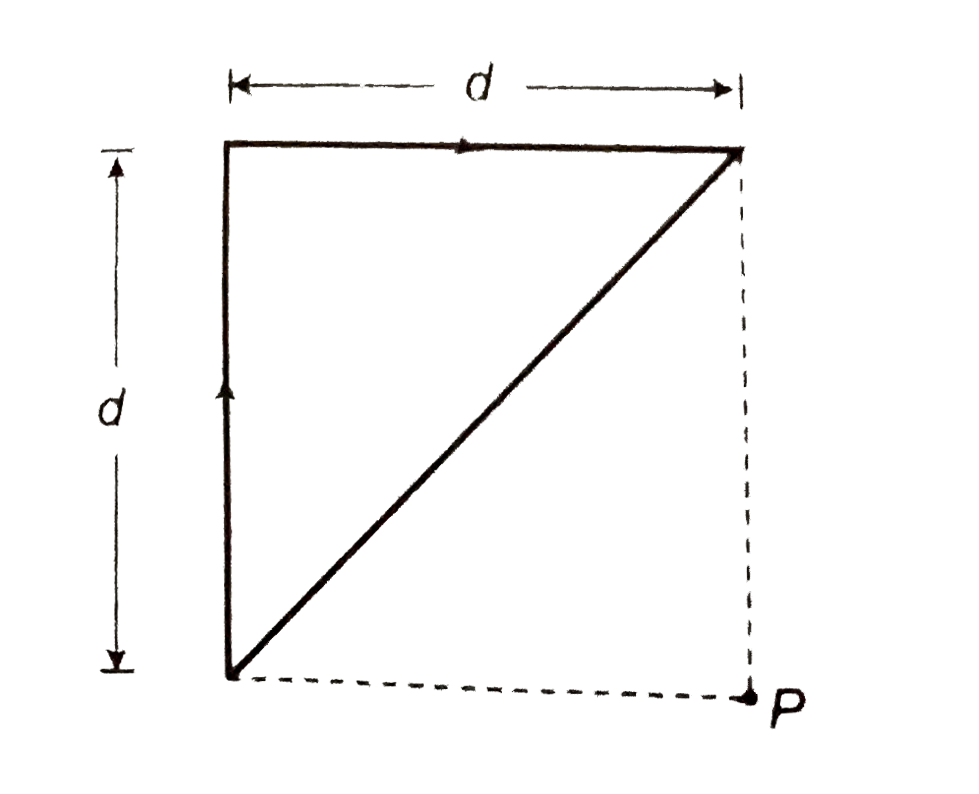
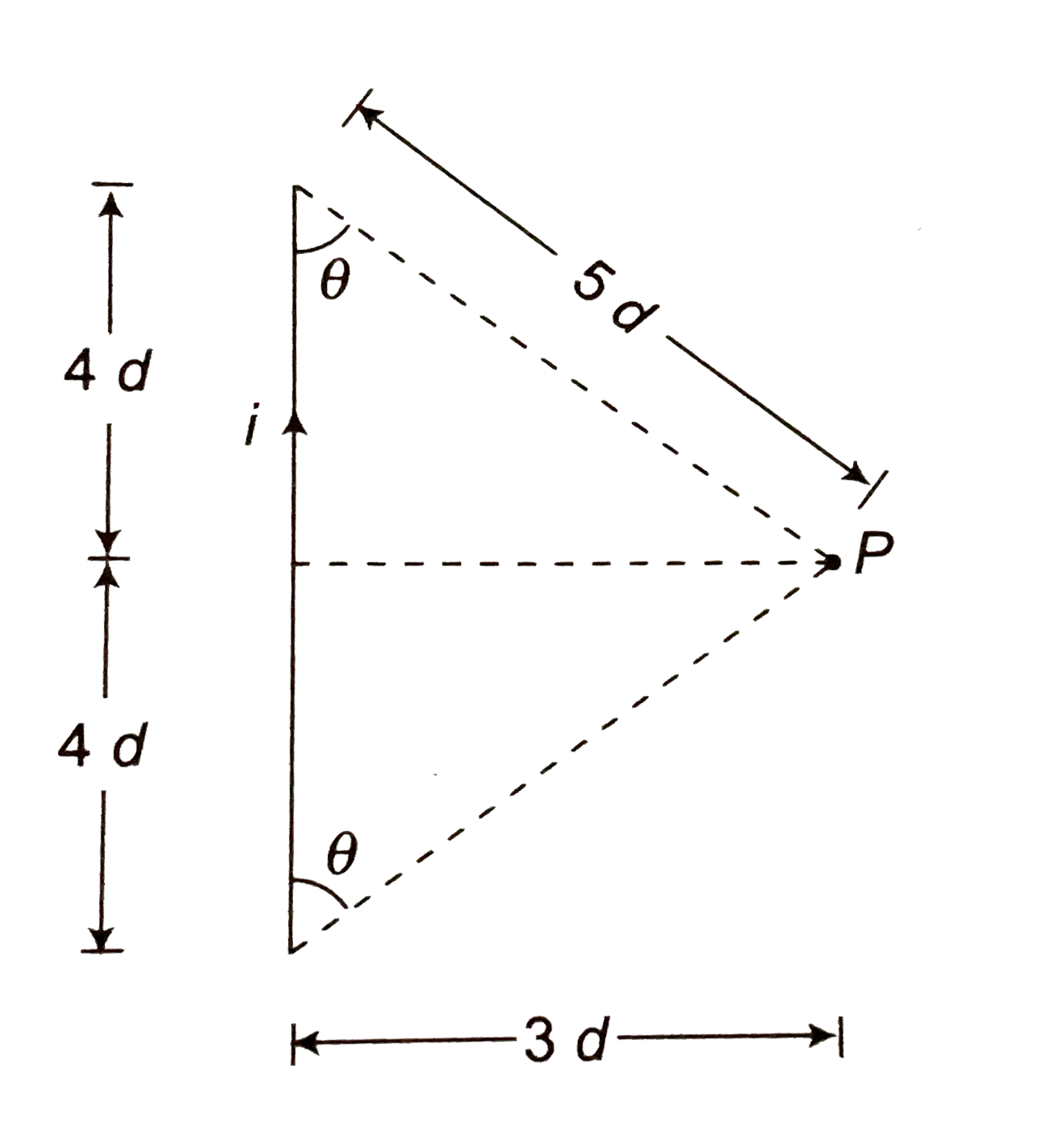
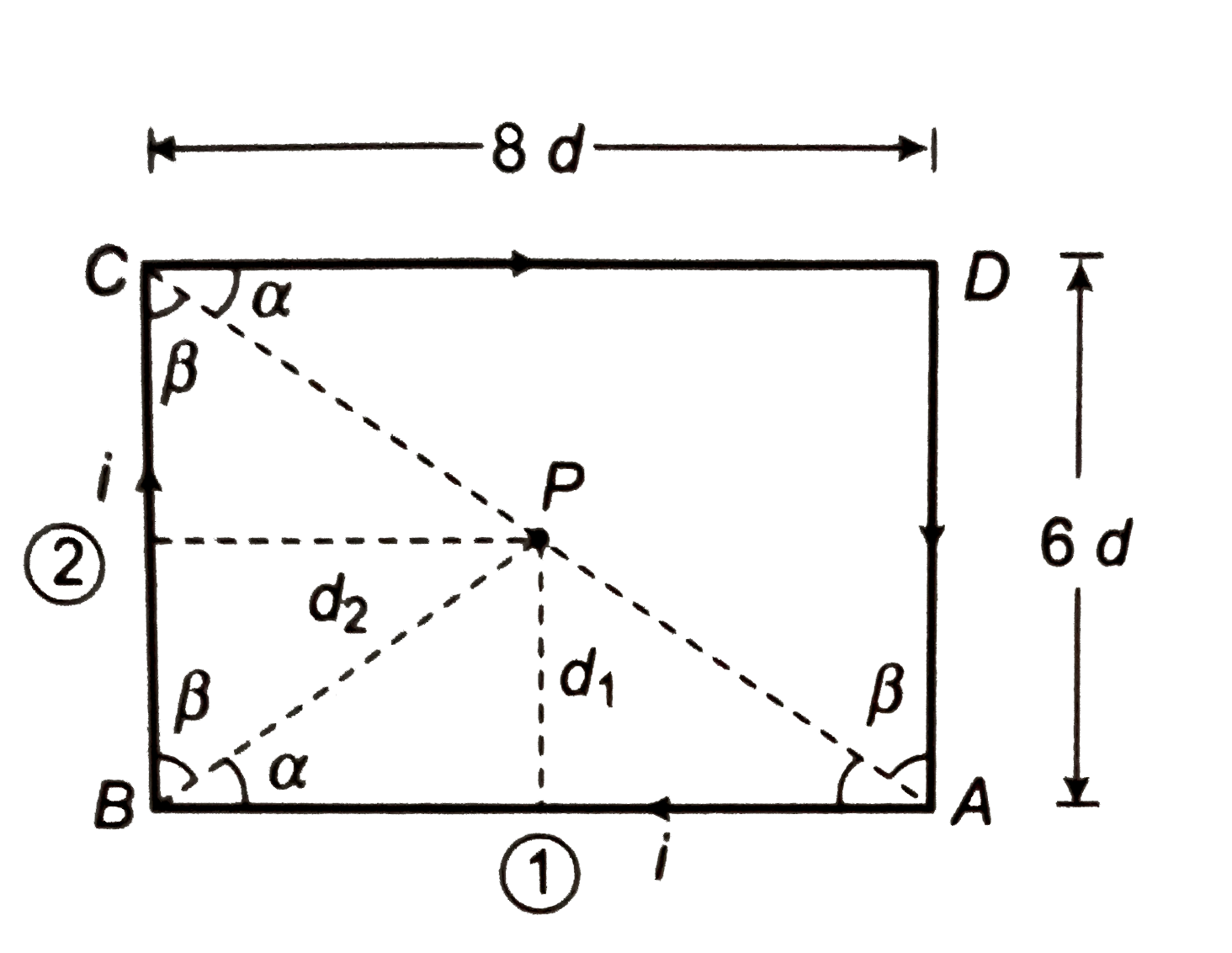
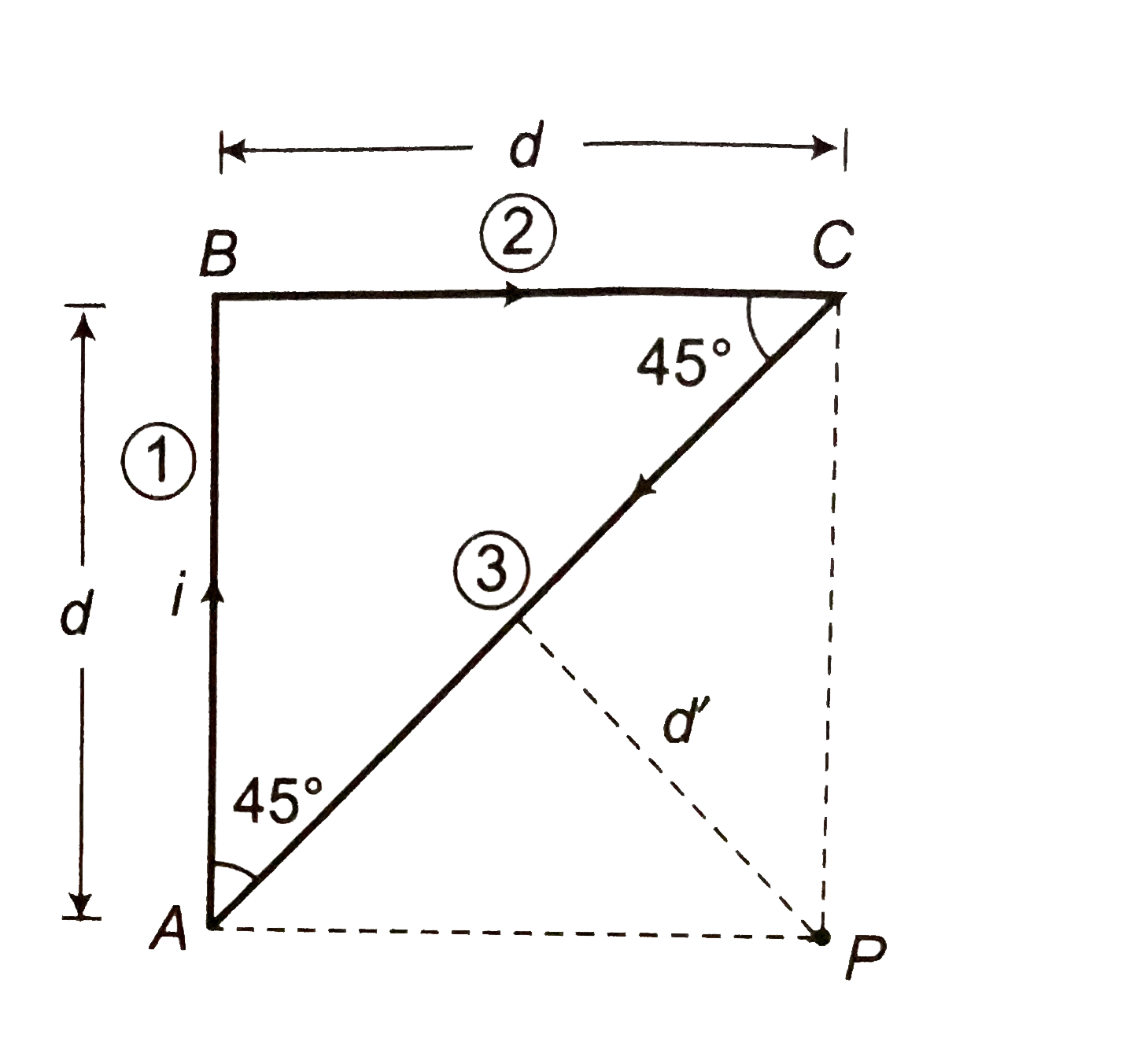
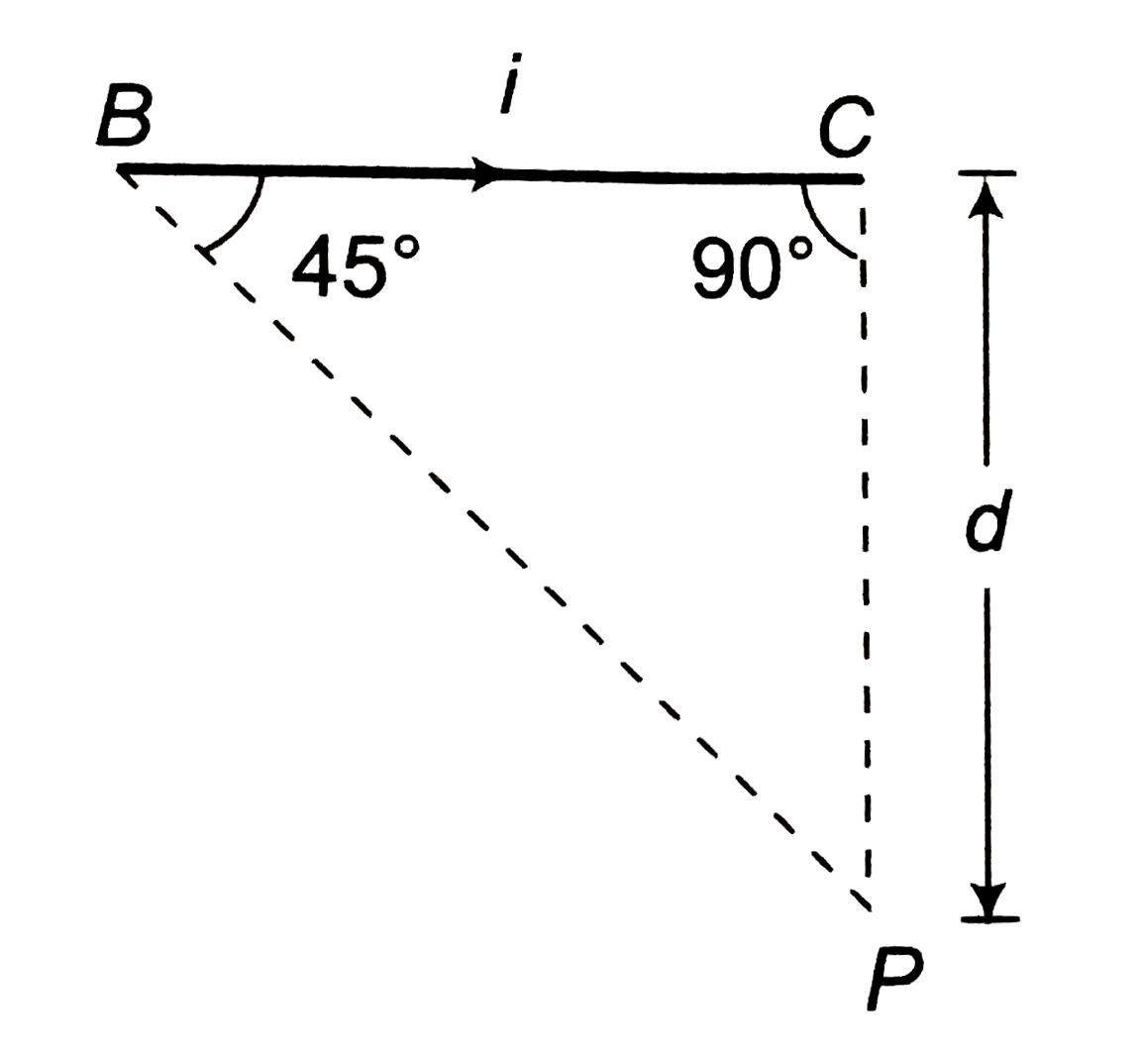
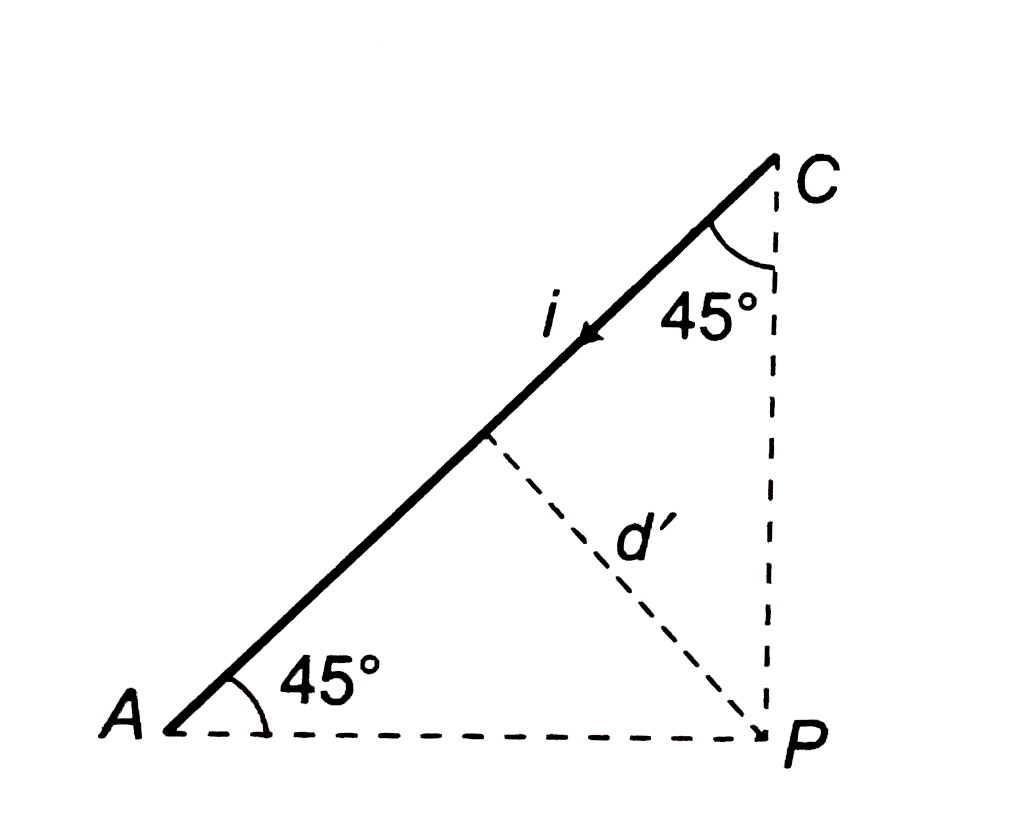
- Find magnitude and direction of magnetic field at point P in the follo...
Text Solution
|
- The magnetic field at the origin due to a current element I vec(dl) pl...
Text Solution
|
- Consider three quantities x=E/B, y=sqrt(1/(mu(0)epsilon(0))) and z=1/(...
Text Solution
|
- If C the velocity of light, which of the following is correct?
Text Solution
|
- A vertical wire carriers a current upwards. The magnetic field at a po...
Text Solution
|
- A moving charge produces
Text Solution
|
- A circular loop is kept in that vertical plane which contains the nort...
Text Solution
|
- O is mid-point of AB. The magnetic field at O is
Text Solution
|
- An infinetely long conductor PQR is bent to from a right angle as show...
Text Solution
|
- A long straight wire carries the current along +ve x-direction. Consid...
Text Solution
|
- A straight section PQ of a circuit lise along the X-axis from x=-a/2 t...
Text Solution
|
- A horizontal overheadpowerline is at height of 4 m from the ground and...
Text Solution
|
- AB and CD are long staright conductors, distance d apart, carrying a c...
Text Solution
|
- A straight conductor carriers a current alon the z-axis Consider the p...
Text Solution
|
- A long wire carrying i is bent to form a plane angle theta.Find the ma...
Text Solution
|
- A wire carrying current I is shaped as shown. Section AB is a quarter ...
Text Solution
|
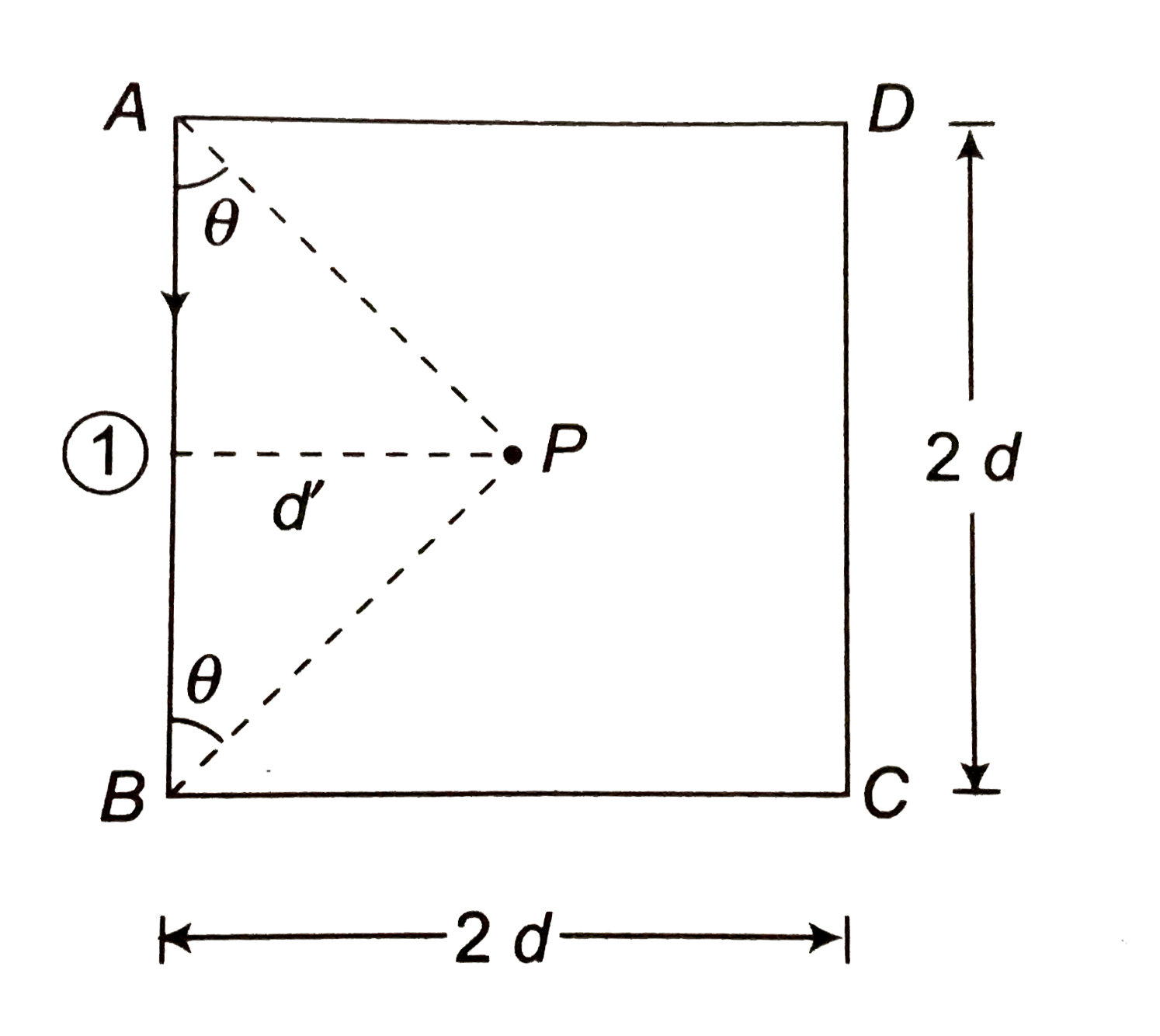
- ABCD is a square loop made of a uniform conducting wire. A current ent...
Text Solution
|
- In the loop shown, all curved sections are either semicircles or quart...
Text Solution
|
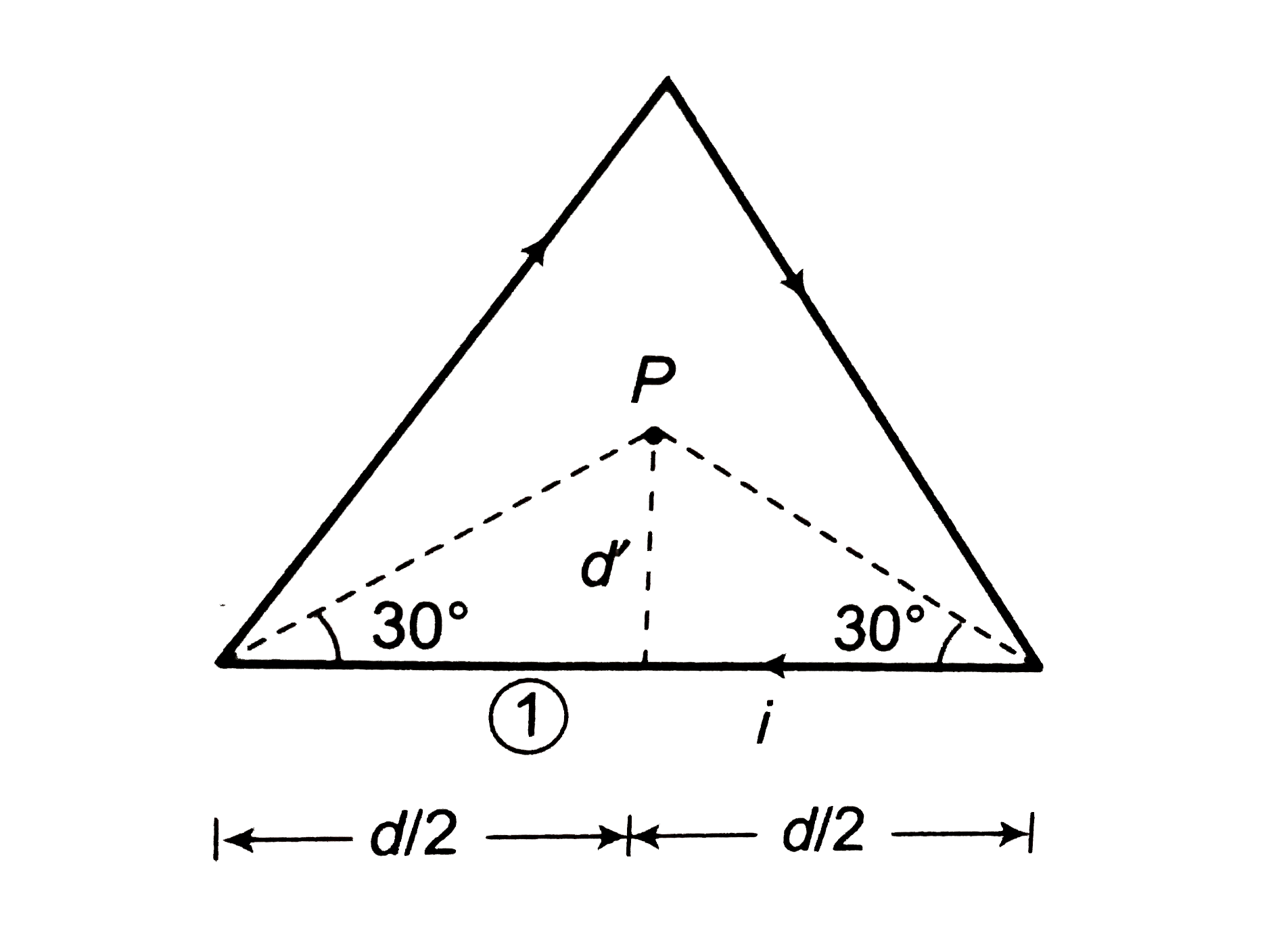
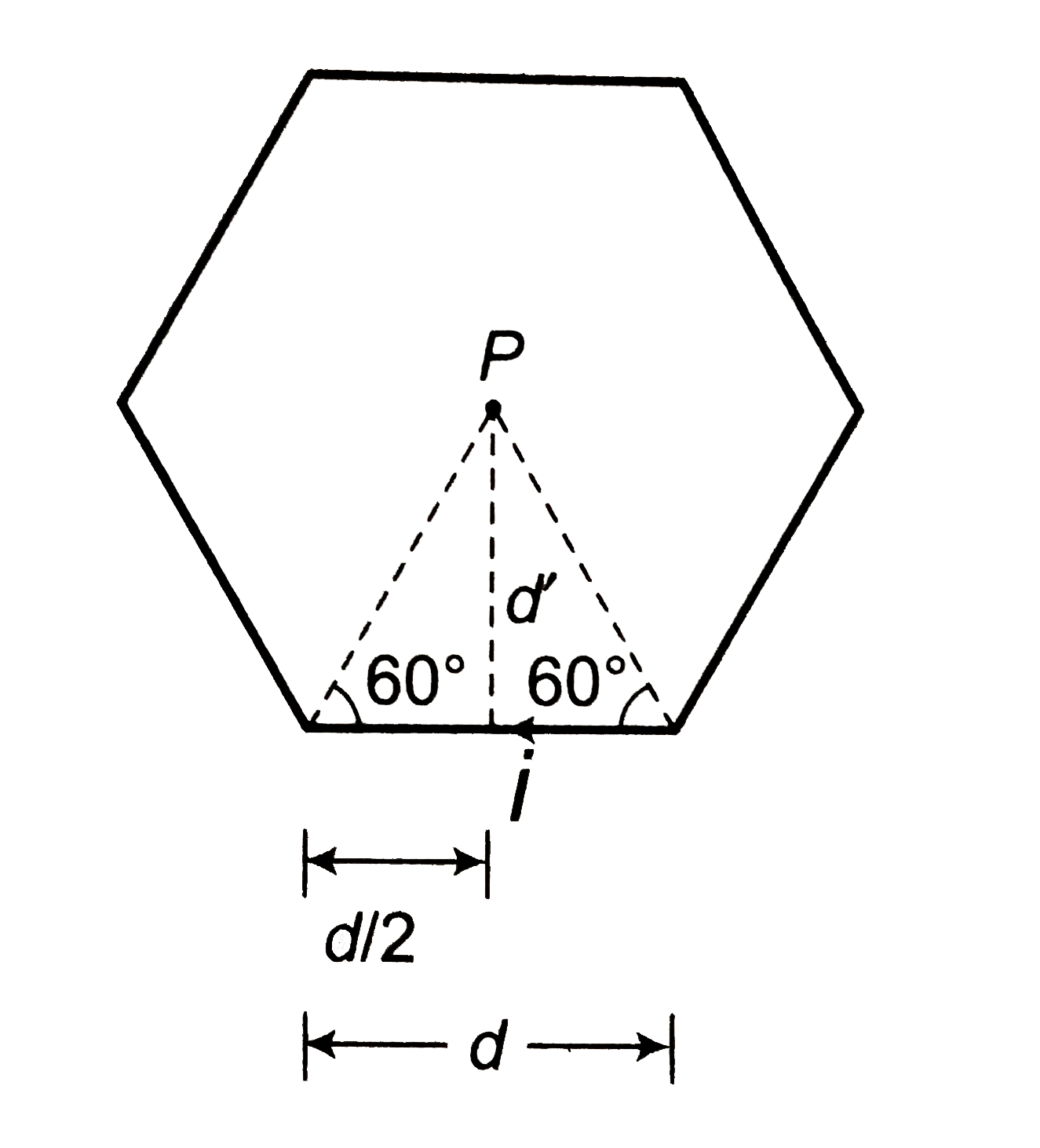
- Evaluate magnitude and direction of magnetic field at a point P in the...
Text Solution
|
- A cell is connected between the point A and C of a circular conductor ...
Text Solution
|
- A battery is connected between two points A and B on the circumference...
Text Solution
|