A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
ELECTRO MAGNETIC INDUCTION
NARAYNA|Exercise Single Answer Questions Level -V|11 VideosELECTRO MAGNETIC INDUCTION
NARAYNA|Exercise Comprehension Type Questions|22 VideosELECTRO MAGNETIC INDUCTION
NARAYNA|Exercise Level - III|64 VideosELECTRIC CHARGES AND FIELDS
NARAYNA|Exercise EXERCISE -4|43 VideosELECTRO MAGNETIC WAVES
NARAYNA|Exercise LEVEL-II(H.W)|14 Videos
Similar Questions
Explore conceptually related problems
NARAYNA-ELECTRO MAGNETIC INDUCTION-NCERT Based Questions
- A square of side L meters lies in the x-y plane in a region, where the...
Text Solution
|
- A loop made of straight edegs has six corners at A(0,0,0), B(L, O,0) C...
Text Solution
|
- A cylindrical bar magnet is rotated about its axis (Figure). A wire is...
Text Solution
|
- There are two coils A and B as shown in Figure. A current starts flowi...
Text Solution
|
- Same as problem 4 except the coil A is made to rotate about a vertical...
Text Solution
|
- The self inductance L of a solenoid of length l and area of cross-sect...
Text Solution
|
- Consider a magnet surround by a wire with an on// of switch S (figure)...
Text Solution
|
- A wire in the form of a tightly would solenoid is connected to a DC so...
Text Solution
|
- A solenoid is connected to a battery so that a steady current flows th...
Text Solution
|
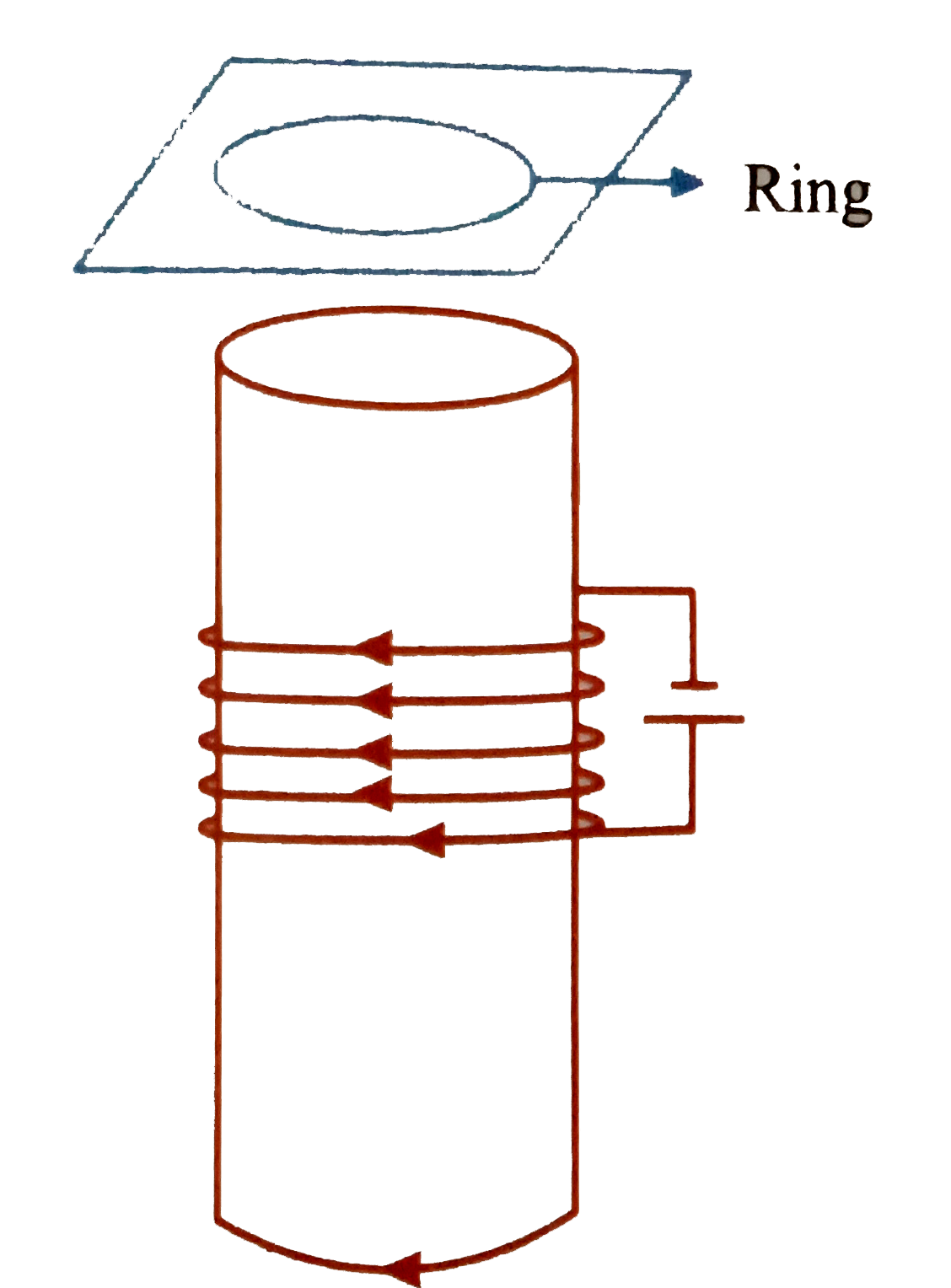
- Consider a metal ring kept on top of a fixed solenoid (say on a carboa...
Text Solution
|