Similar Questions
Explore conceptually related problems
Recommended Questions
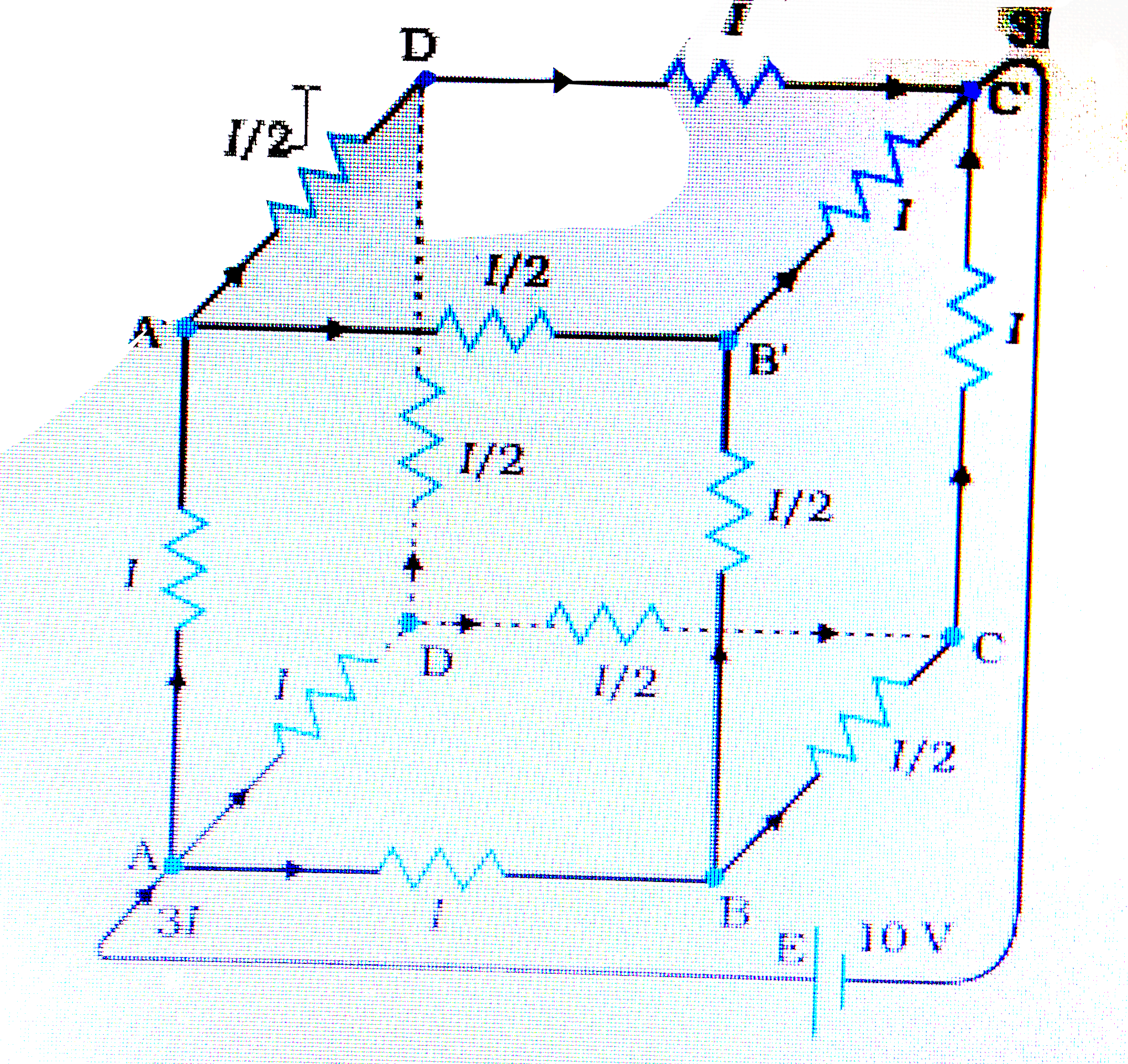
- Battery of 10 V and negligible internal resistance is connected across...
Text Solution
|
- A battery of 15 V and negligible internal resistance is connected acro...
Text Solution
|
- Battery of 10 V and negligible internal resistance is connected across...
Text Solution
|
- 10 V तथा नगण्य आंतरिक प्रतिरोध की बैटरी एक घनीय परिपथ जाल ( नेट...
Text Solution
|
- A network of resistor is connected to a 16 V battery with internal res...
Text Solution
|
- A network of resistor is connected to a 16 V battery with internal res...
Text Solution
|
- निम्न चित्र के अनुसार 1 Omega आंतरिक प्रतिरोध के 16 V कि एक बैटरी स...
Text Solution
|
- 10 V तथा नगण्य आंतरिक प्रतिरोध कि बैटरी एक घनीय परिपथ जाल ( नेटवर...
Text Solution
|
- Twelve wires, each of resistance 1Omega are connected to form a skelet...
Text Solution
|