Similar Questions
Explore conceptually related problems
Recommended Questions
- A and B are two concentric spherical shells made of conductor. Their r...
Text Solution
|
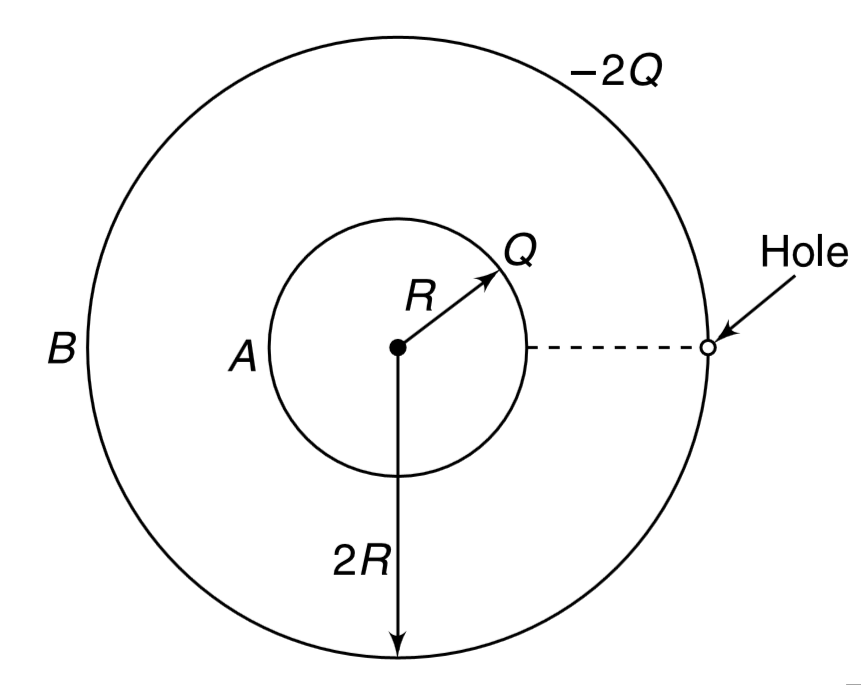
- Two concentric conducting shells A and B are of radii R and 2R . A cha...
Text Solution
|
- There are two concentric spherical shell of radii r and 2r . Initially...
Text Solution
|
- There are two concentric spherical shell of radii r and 2r . Initially...
Text Solution
|
- Consider two concentric metalic shell's of radii R and 2R. The inner s...
Text Solution
|
- A and B are two concentric spherical shells made of conductor. Their r...
Text Solution
|
- In a spherical capacitor,-we have two concentric spherical shells, the...
Text Solution
|
- Three concentric conducting spherical shells carry charges as : +4Q on...
Text Solution
|
- Two concentric spherical conducting shells of radii r and R (r lt R ) ...
Text Solution
|