Similar Questions
Explore conceptually related problems
Recommended Questions
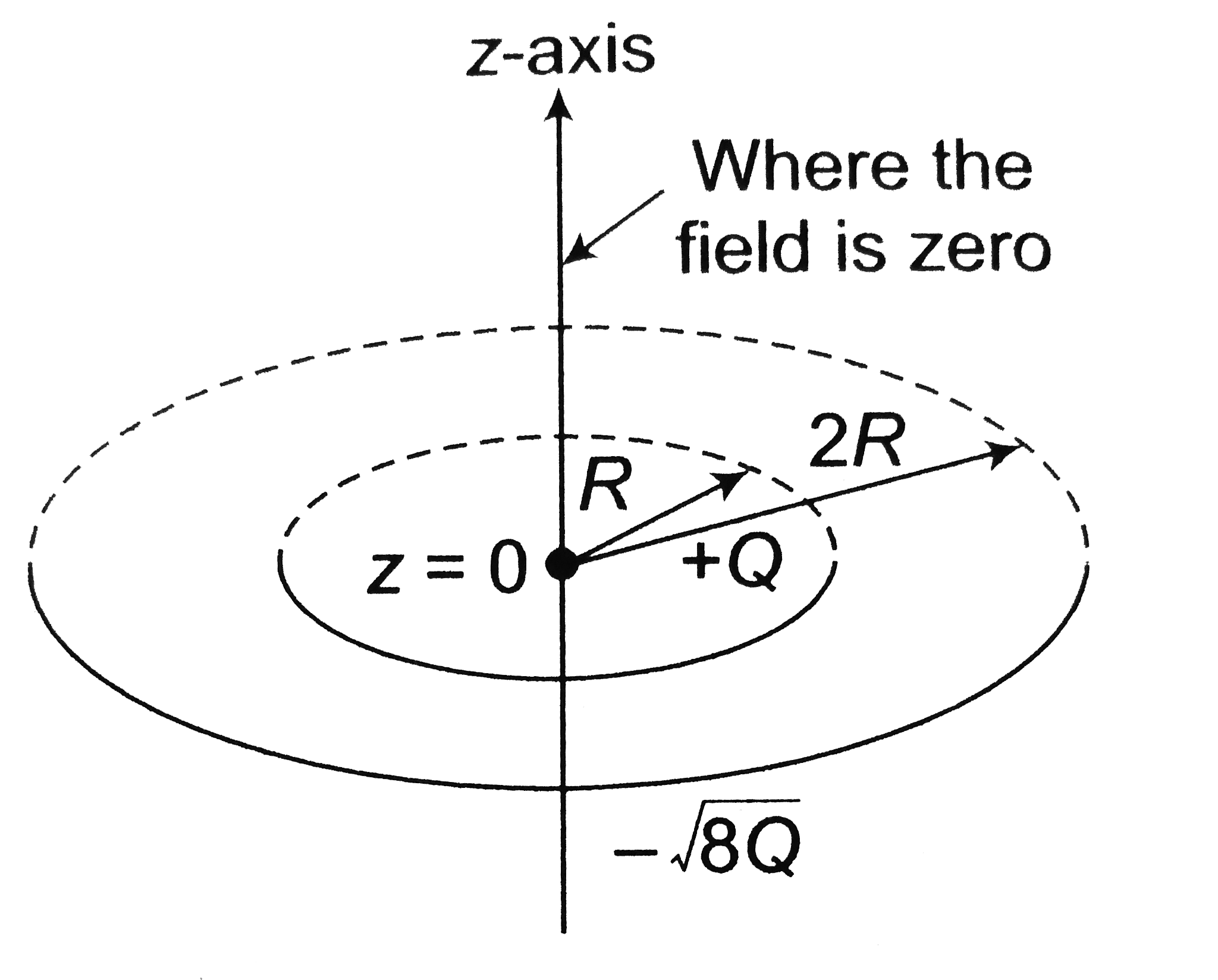
- Two concentric rings, one of radius R and total charge +Q and second o...
Text Solution
|
- A ring of radius a contains a charge q distributed uniformly over its ...
Text Solution
|
- A ring of radius R has charge -Q distributed uniformly over it. Calcul...
Text Solution
|
- Two concentric rings, one of radius R and total charge +Q and second o...
Text Solution
|
- An electric dipole is kept on the axis of a uniformly charged ring at ...
Text Solution
|
- An unchanged conducting sphere of radius R is placed near a uniformly ...
Text Solution
|
- A short dipole is placed on the axis of a uniformly charged ring (tota...
Text Solution
|
- yz-तल में रखे R त्रिज्या के किसी रिंग का केन्द्र मूलबिंदु (origin ) पर...
Text Solution
|
- R त्रिज्या के कुचालक पदार्थ से बने किसी आवेशित वृत्ताकर रिं...
Text Solution
|