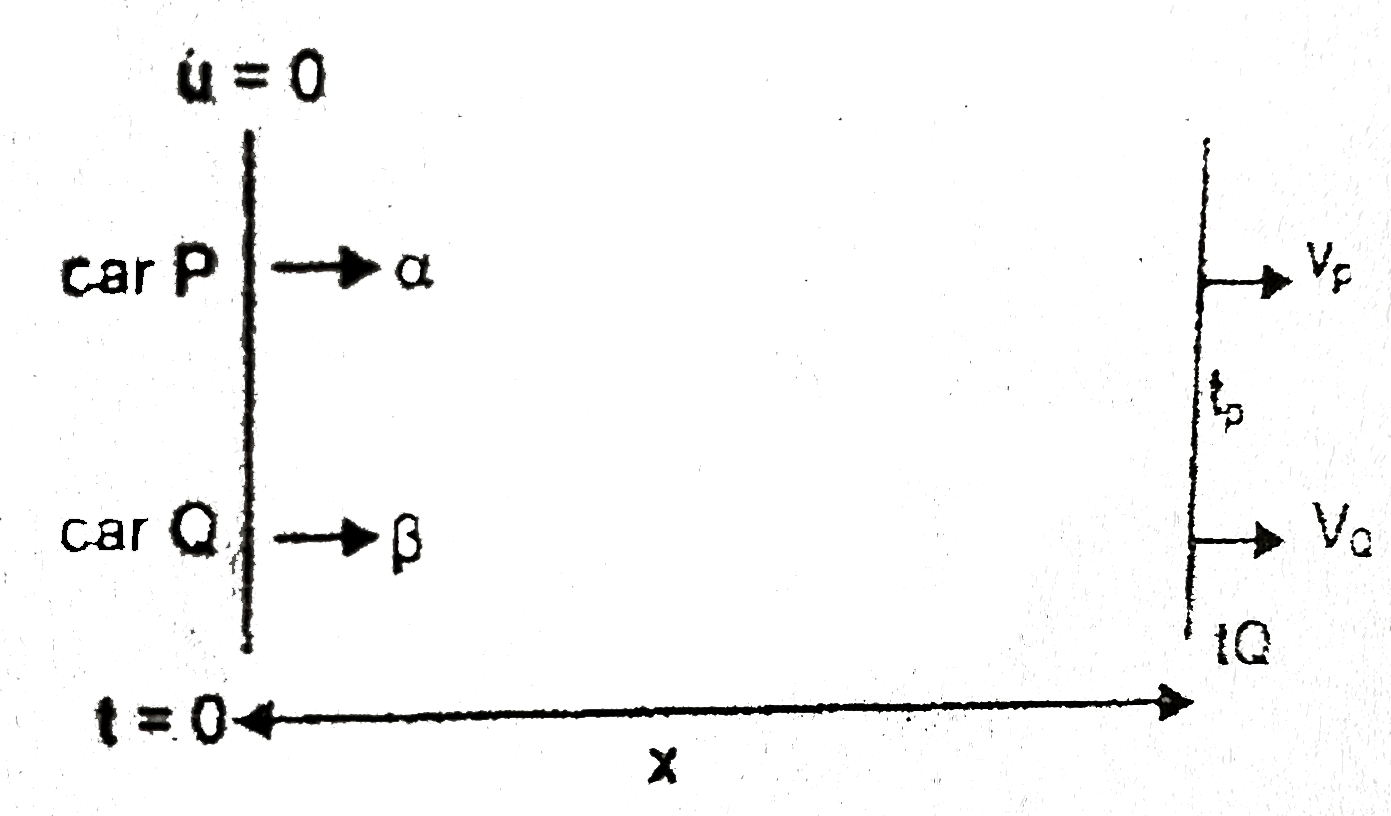A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- In a car race, car P takes time t(0) less than car Q and passes the fi...
Text Solution
|
- In a car race, car A takes a time t less than car B at the finish and ...
Text Solution
|
- In a car race, A takes a time of t s, less than car B at the finish an...
Text Solution
|
- In a car race, car A takes t0 time less to finish than car B and passe...
Text Solution
|
- In a car race, car P takes time t(0) less than car Q and passes the fi...
Text Solution
|
- In a car race car A takes t(0) time less to finish than car B and pase...
Text Solution
|
- In a car race, car A takes time t less than car B and passes the finis...
Text Solution
|
- In a car race, car A takes time t less than car B and passes the finis...
Text Solution
|
- In a car race, car A takes time t less than car B and passes the finis...
Text Solution
|