Home
Class 12
PHYSICS
A body which was released from rest, sli...

A body which was released from rest, slides down on an inclined plane of inclination `theta`. The coefficient of friction dowh the plane varies as `mu = kx` where k is a spositive constant and x is the distance moved by the body down the plane. The speed of the body 'v' versus distance 'x' graph will be as :

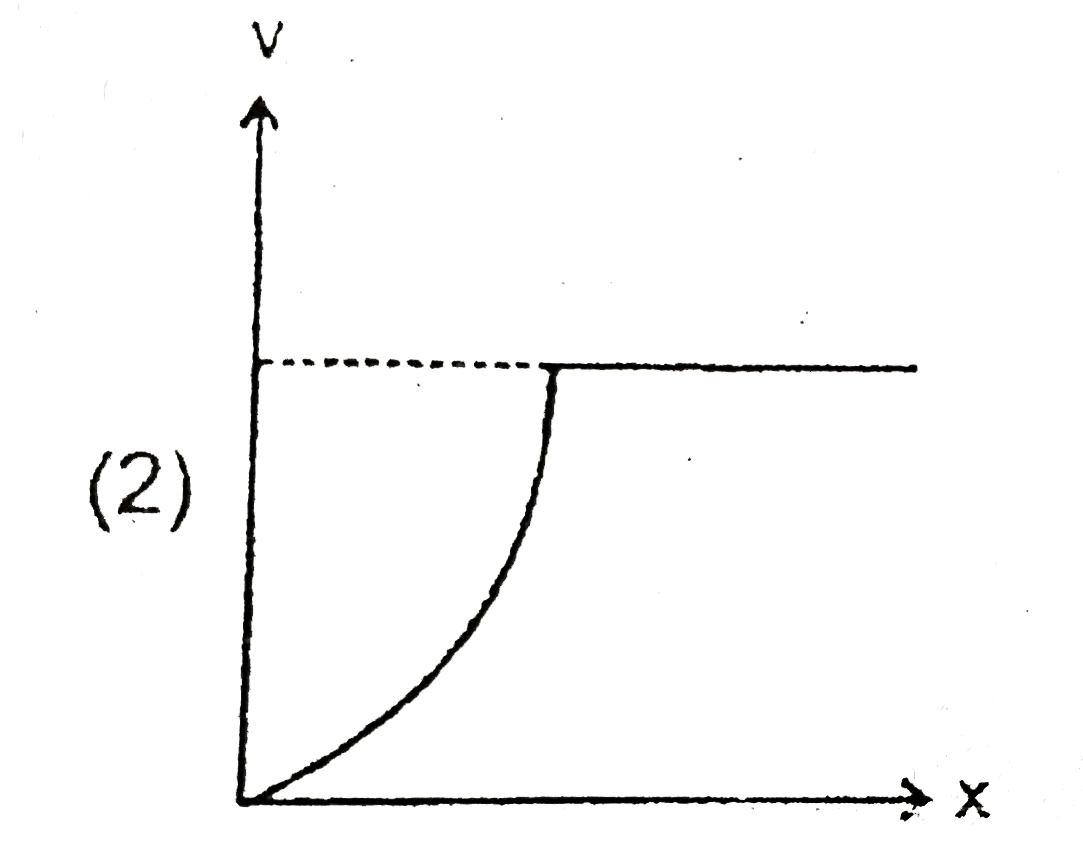
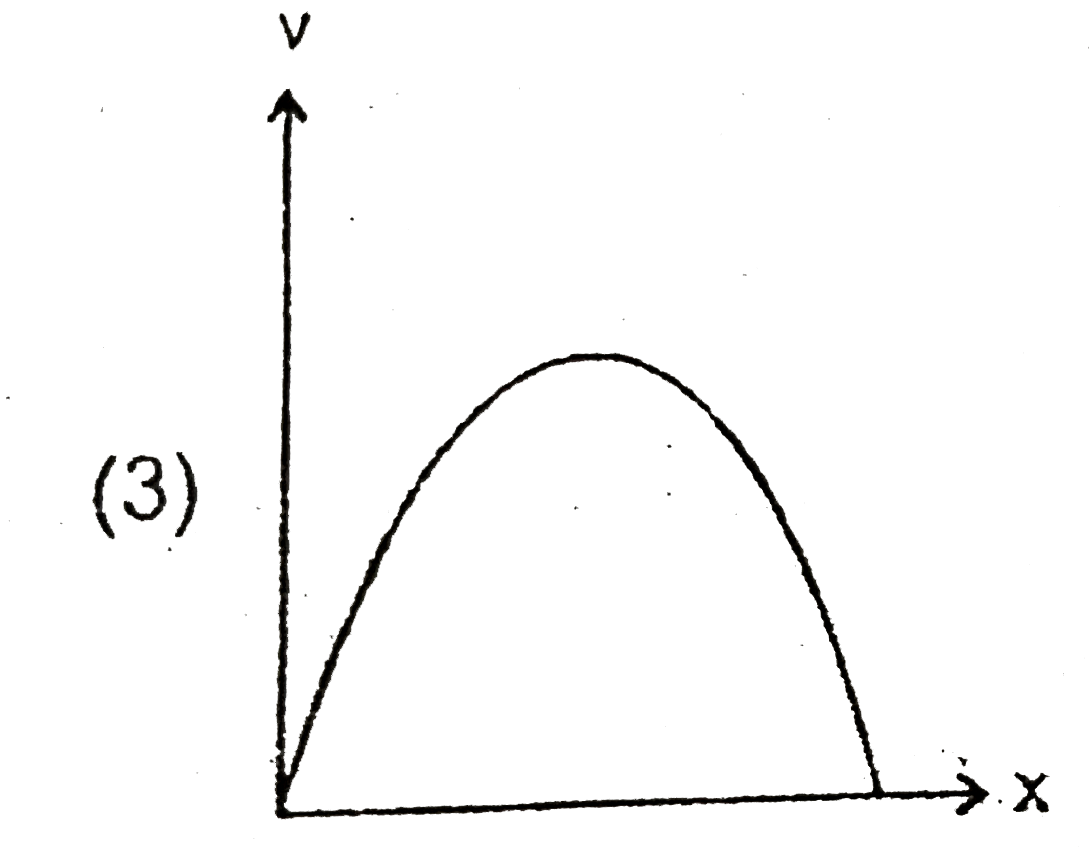
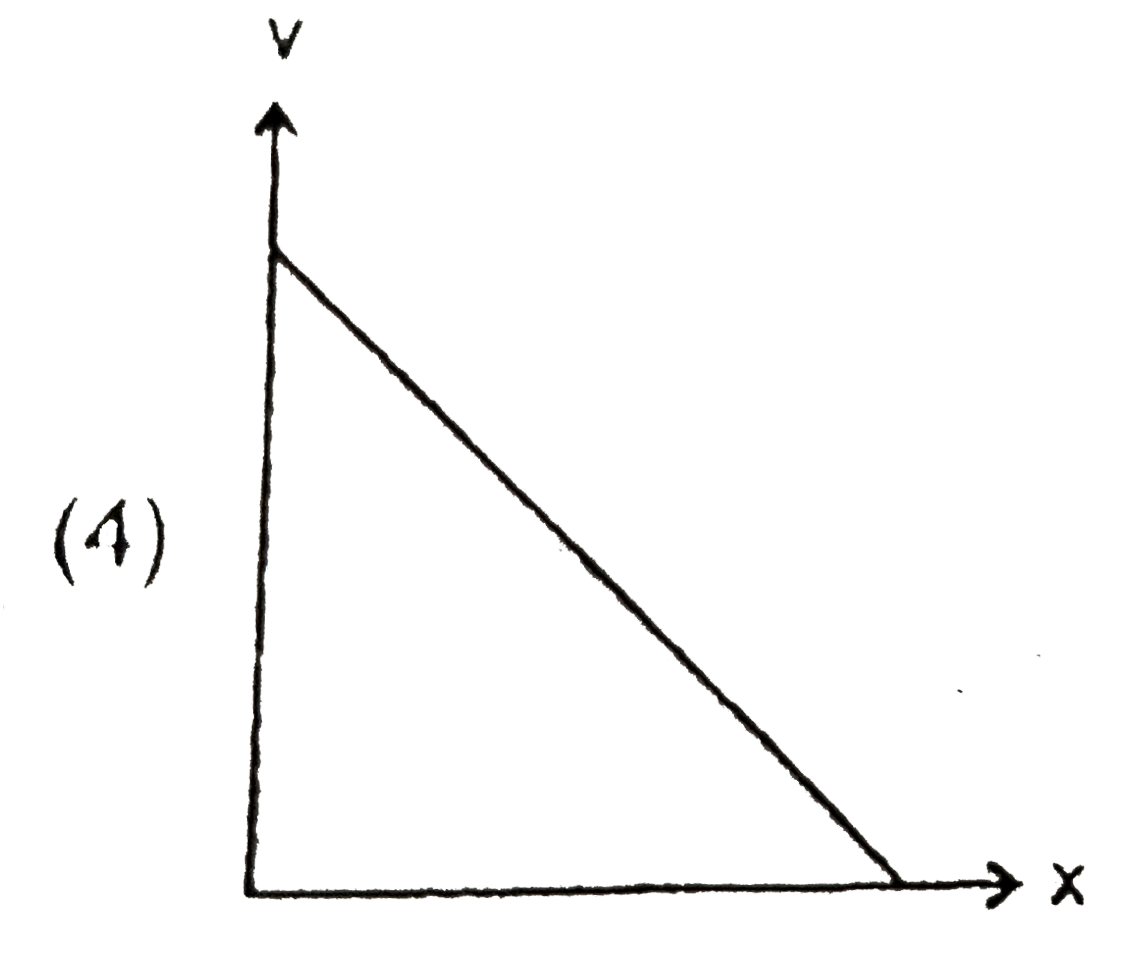
A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
C
A body which ………..
`a = g (sin theta - kx cos theta)`
`theta = constt`.
`v = g(sin theta x - (kx^(2))/(2)cos theta)`

Hence required graph will be as
Promotional Banner

Similar Questions

Explore conceptually related problems

A body is moving down a long inclined plane of angle of inclination 'theta ' for which the coefficient of friction varies with distance x as mu (x) = kx , where k is a constant . Here x is the distance moved by the body down the plane . The net force on the body will be zero at a distance x_(0) is given by ..........

A body is moving down along inclined plane of angle of inclination theta The coefficient of friction between the body and the plane varies as mu=0.5x where x is the distance moved down the plane. The body will have the maximum velocity when

A body is moving down a long inclined plane of inclination 45^(@) with horizontal. The coefficient of friciton between the body and the plane varies as mu = x//2 , where x is the distance moved down the plane. Initially x=0 & v=0

A block of mass m moves with constant speed down the inclined plane of inclination theta . Find the coefficient of kinetic friction.

A body is moving down a long inclined plane of angle of inclination theta . The coefficient of friction between the body and the plane varies as mu - 0.1 x , where x is the distance moved down the plane. The body will have the maximum velocity when it has travelled a distance x given by :

A body is moving down a long inclined plane in inclination 45^(@) with horizontal. The coefficient of friction between the body and the plane varies as mu=x//2 , where x is the distance moved down the plane. Initially x=0 & v=0 .

When a body of mass M slides down an inclined plane of inclination theta , having coefficient of friction mu through a distance s, the work done against friction is :

A small mass slides down an inclined plane of inclination theta the horizontal the coefficient of friction is m = mu_(0)x , where x is the distance by the mass before it stops is .

A body of mass m slides down a rough plane of inclination alpha . If mu is the coefficient of friction, then acceleration of the body will be

A body of mass m slides down a rough plane of inclination alpha . If mu is the coefficient of friction, then acceleration of the body will be