A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
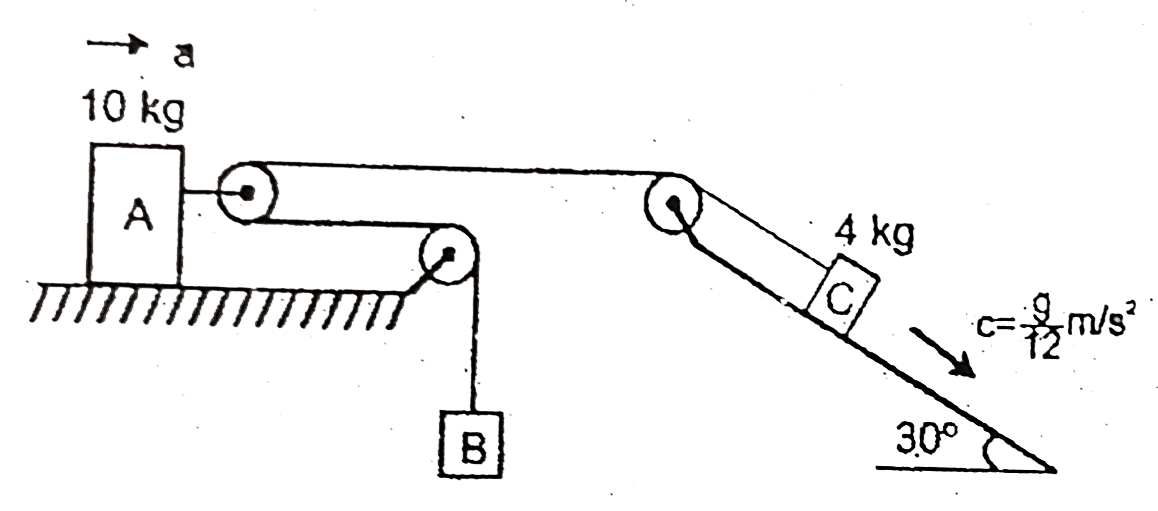
- The acceleration of block 'C' is equal to (g)/(12)m//s^(2) where g is ...
Text Solution
|
- a block is kept on the floor of an elevator at rest. The elevator star...
Text Solution
|
- Consider the situation shown in figure .Both the pulleys and the strin...
Text Solution
|
- The acceleration of block 'C' is equal to (g)/(12)m//s^(2) where g is ...
Text Solution
|
- Find the acceleration of the 6 kg block in the figure. All the surface...
Text Solution
|
- गुरुत्वीय त्वरण 'g' का मान …………….. मीटर/से""^(2) होता है।
Text Solution
|
- In the figure ( g = 10 m//s^(2) ) .Acceleration of 2kg block is :
Text Solution
|
- Pulleys are ideal and string are massless. The masses of blocks are m(...
Text Solution
|
- The weights W and 2W are suspended from the ends of a light string pas...
Text Solution
|