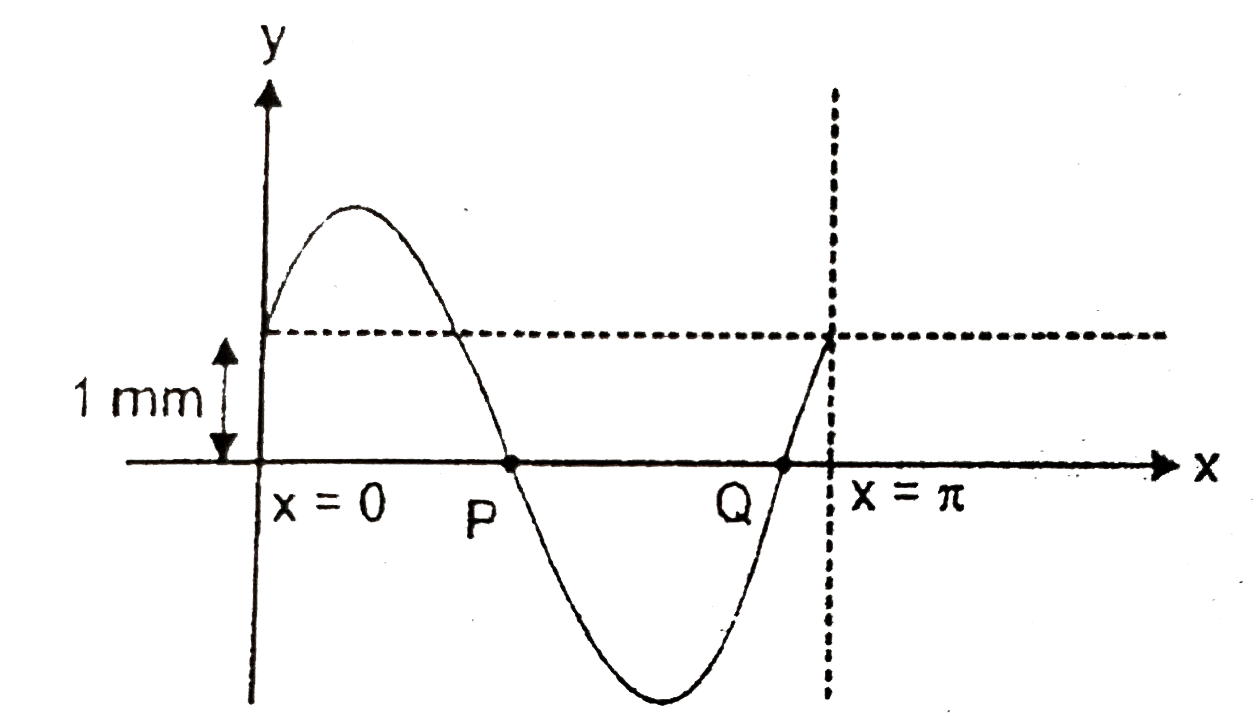
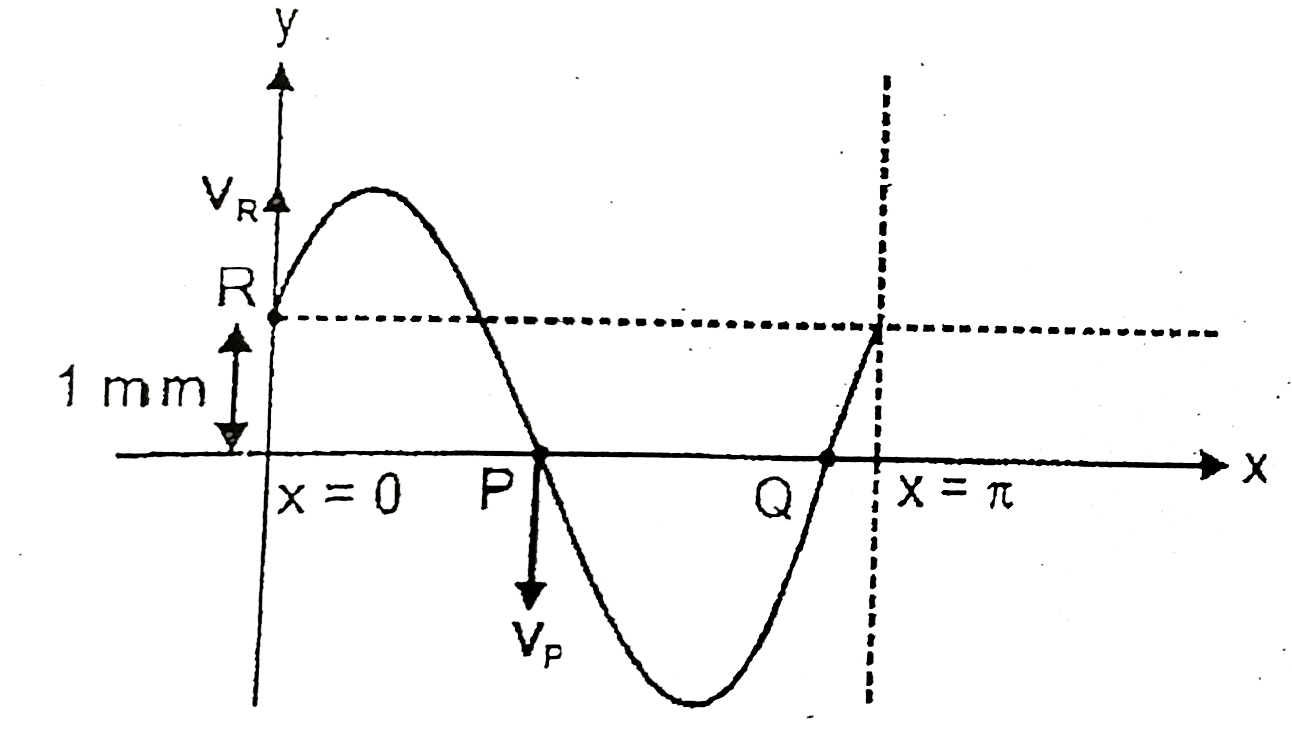A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A transerse sinusodial wave of amplitude 2 mm is setup in a long unifo...
Text Solution
|
- Shows a snapshot of a sinusoidal travelling wave taken at t=0.3s. The ...
Text Solution
|
- A wave is propagating along the length of a string taken as positive x...
Text Solution
|
- Stationary wave is setup in a uniform string clamped at both the ends....
Text Solution
|
- Stationary wave is setup in a uniform string clamped at both the ends....
Text Solution
|
- Stationary wave is setup in a uniform string clamped at both the ends....
Text Solution
|
- A transerse sinusodial wave of amplitude 2 mm is setup in a long unifo...
Text Solution
|
- A travelling wave y=A sin (kx- omega t +theta ) passes from a heavier ...
Text Solution
|
- A transverse wave of equation y = 2 sin (0.01 x +30 t) moves on a stre...
Text Solution
|