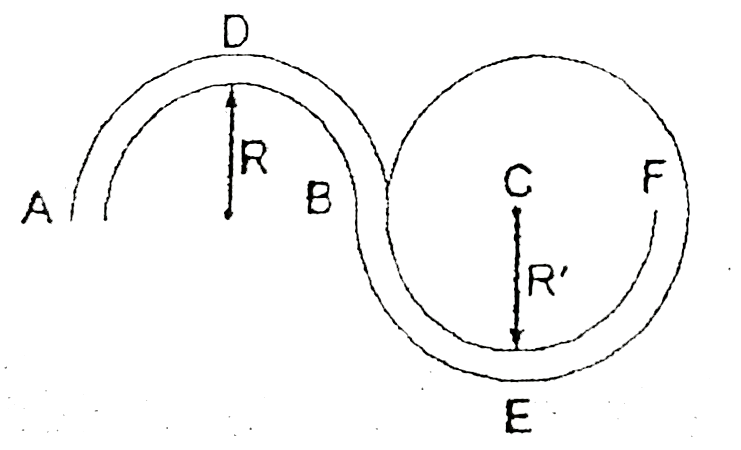A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
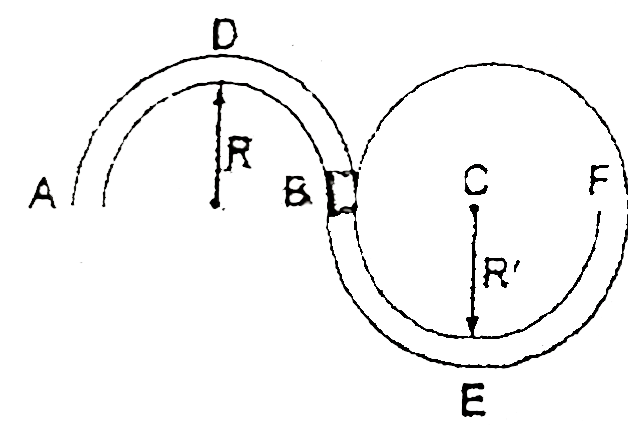
- In the figure ADB & BEF are two fixed circular paths. A block of mass ...
Text Solution
|
- As shown in figure BEF is a fixed vertical circular tube. A block of m...
Text Solution
|
- In the figure ADB & BEF are two fixed circular paths. A block of mass ...
Text Solution
|
- एक सर्कस में मोटरसाइकिल चालक ऊर्ध्वाधर ताल में R त्रिज्या के वृताकार प...
Text Solution
|
- द्रव्यमान m का कण बल F के प्रभाव में त्रिज्या r के वृत्ताकार पथ में न...
Text Solution
|
- द्रव्यमान m एवं आवेश q का एक आवेशित कण एकसमान चुम्बकीय क्षेत्र B में त...
Text Solution
|
- In a fixed quarter circular track of radius R which lies in a vertical...
Text Solution
|
- A fighter aircraft rotates in a vertical circular path. What will be t...
Text Solution
|
- R At the highest point for rotation in a vertical circular path of rad...
Text Solution
|