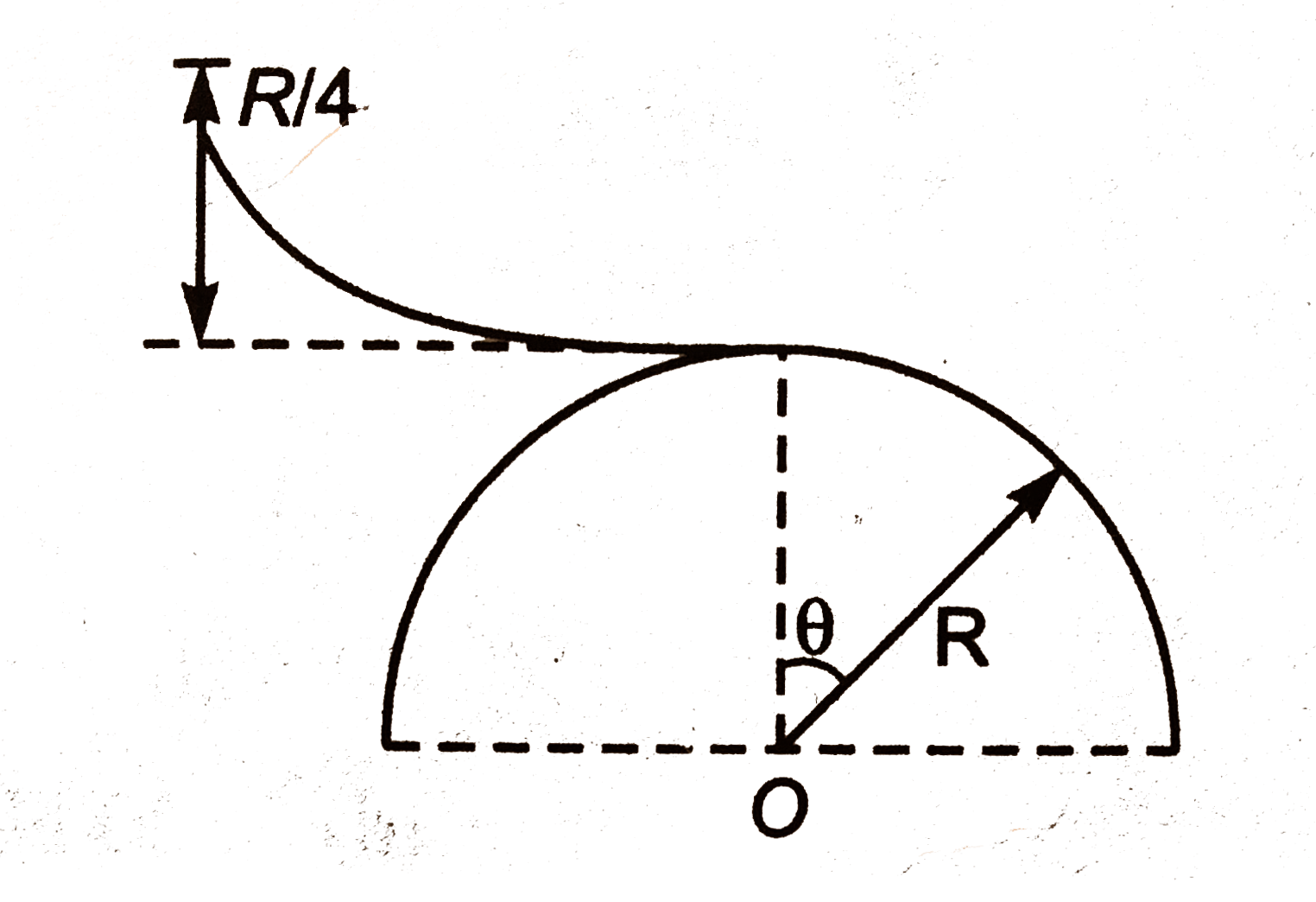A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A skier plane to ski a smooth fixed hemisphere of radius R . He starts...
Text Solution
|
- A skier plane to ski a smooth fixed hemisphere of radius R . He starts...
Text Solution
|
- A small sphere D of mass and radius rols without slipping inside a lar...
Text Solution
|
- A particle of mass m is released from the top of a smooth hemisphere o...
Text Solution
|
- A particle is released from the top of the smooth hemisphere R as show...
Text Solution
|
- A particle of mass m initially at rest starts moving from point A on t...
Text Solution
|
- A particle P is initially at rest on the top pf a smooth hemispherical...
Text Solution
|
- A skier plans to ski a smooth fixed hemisphere of radius R He starts f...
Text Solution
|
- A mass m is released with a horizontal speed v from the top of a smoot...
Text Solution
|