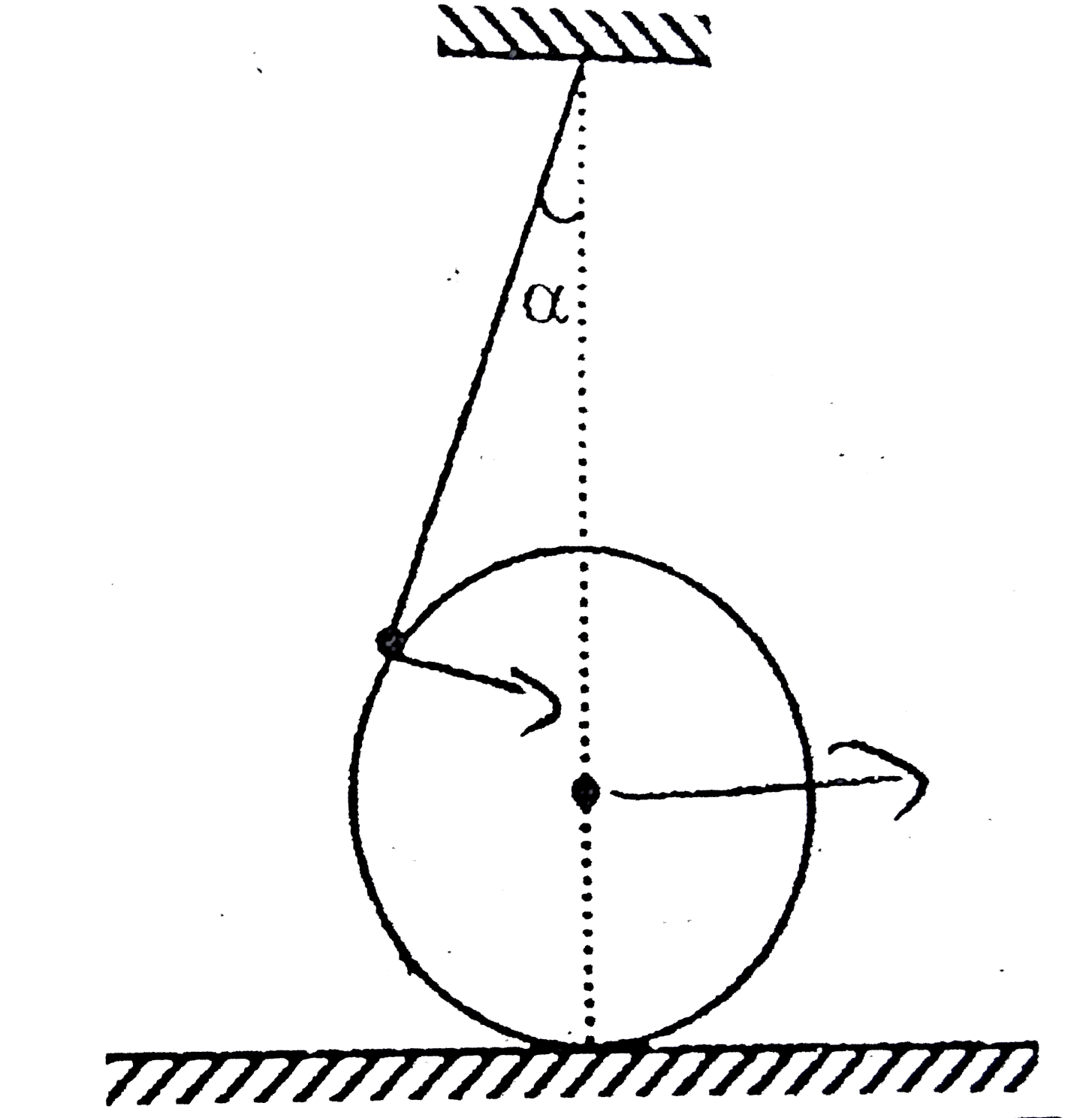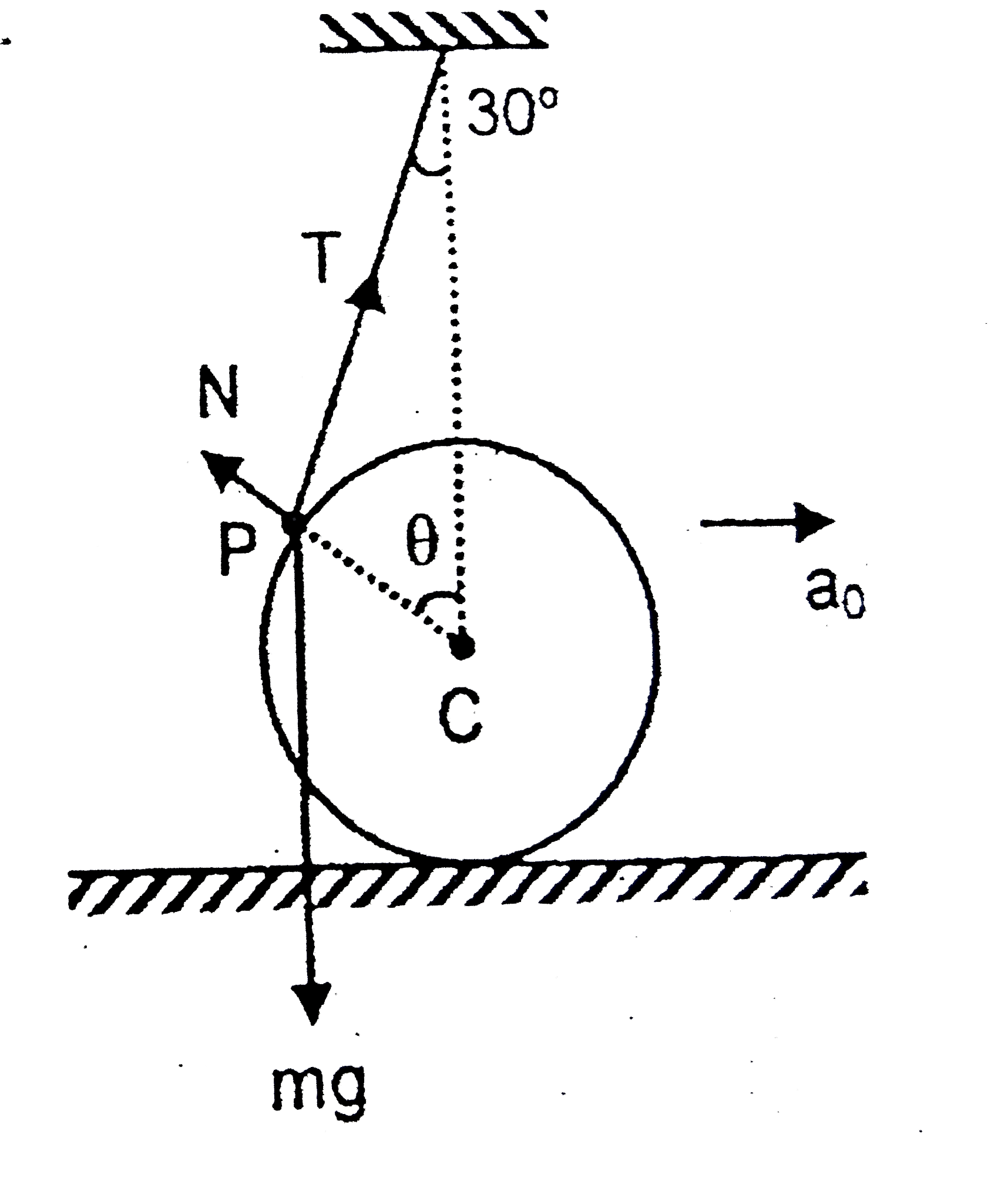A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A sphere of mass M is held at rest on a horizontal floor. One end of a...
Text Solution
|
- A string of length L is fixed at one end and carries a mass M at the o...
Text Solution
|
- A sphere of mass M is held at rest on a horizontal floor. One end of a...
Text Solution
|
- A string of length 1 m is fixed at one end and carries a mass of 100 g...
Text Solution
|
- A sphere of mass M is held at rest on a horizontal floor. One end of a...
Text Solution
|
- A cylinder C rests on a horizontal surface. A small particle of mass m...
Text Solution
|
- A solid uniform sphere of mass M and radius R can rotate about a fixed...
Text Solution
|
- A particle of mass m is attached to one end of a light inextensible st...
Text Solution
|
- A particle of mass m is attached to one end of a light inextensible st...
Text Solution
|