Home
Class 12
PHYSICS
Figure shows a circular frications trck ...

Figure shows a circular frications trck of radius `R`, centred at point `O`. A particle of mass `M` is released from point `A (OA = R//2)`. After collision with the track, the particle moves along on the track. Then the coefficient of restitution `e` is.

A

`0.2`

B

`0.5`

C

`1`

D

zero

Text Solution

Verified by Experts

The correct Answer is:
D
`cos theta = (1)/(2) rArr theta = (pi)/(3)`
(a) After collision the particle moves along the track. This means there is no normal component of velocity, Hence `e = 0`
(b) Just before collision, the compoenents of velocity along the normal and along the tangent are
`u_(n) = u sin theta`
`u_(t) = u cos theta`

During collision `u_(t)` does not change. The normal component of velocity becomes `eu_(n)` along `overset(vec)(B)O`.

Question says that velocity of the particle is horizontal after collision, which mean s`u_(t) cos theta = eu_(n) sin theta`
`u cos2 theta = eu sin2theta rArr e = cot^(2)'(pi)/(3) = (1)/(3)`
Promotional Banner

Similar Questions

Explore conceptually related problems

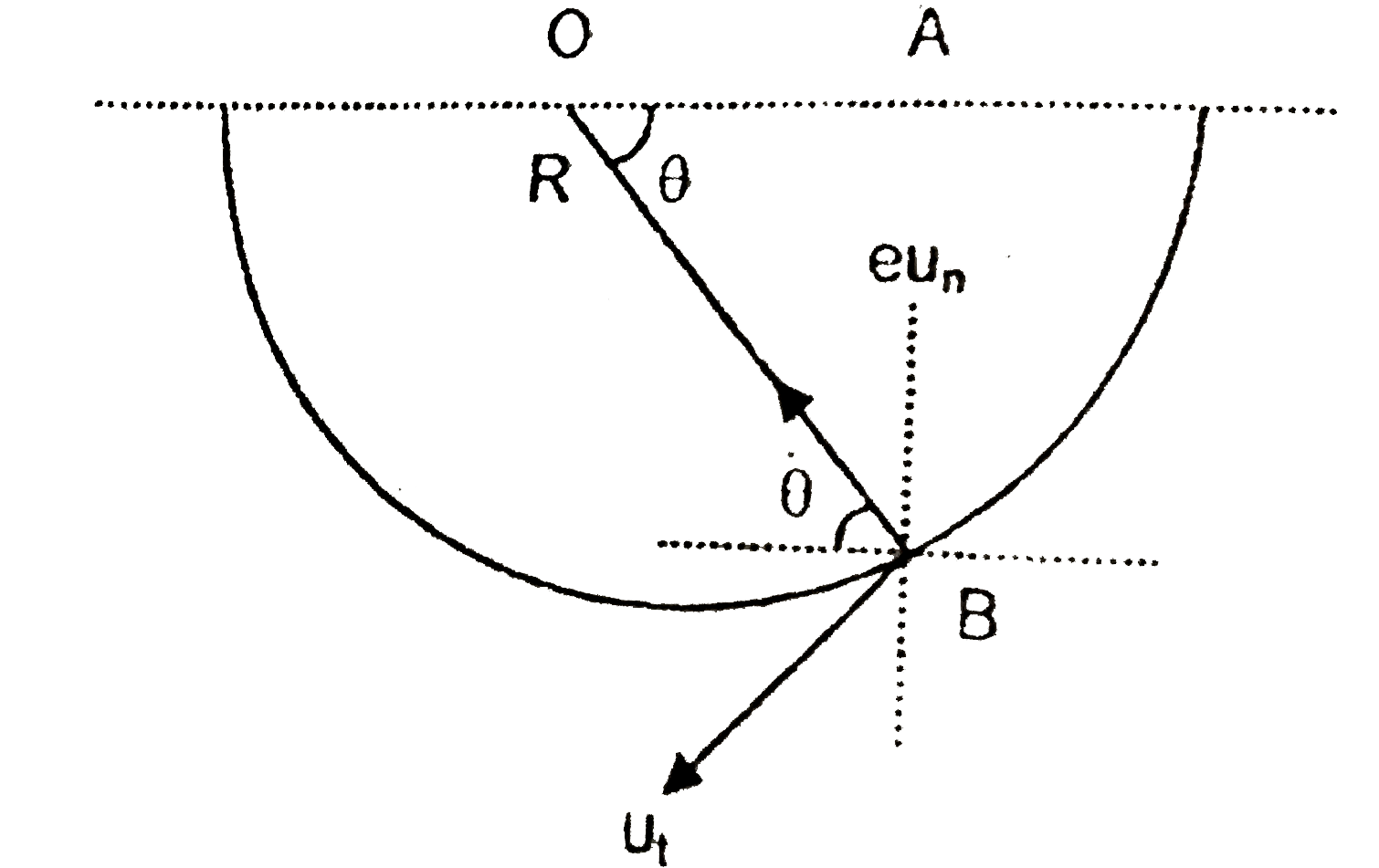
Figure shows a circular frictionless track of radius R, centred at point O. A particle of mass M is released from point A (OA = R//2) . After collision with the track, the particle moves along the track. (a) Find the coefficient of restitution e . (b) What will be value of e if the velocity of the particle becomes horizontal just after collision ?

A circular ring of mass M and radius R is placed in YZ plane with centre at origin. A particle of mass m is released from rest at a point x = 2R. Find the speed with which it will pass the centre of ring .

A particle of mass m, collides with another stationary particle of mass M. If the particle m stops just after collision, then the coefficient of restitution for collision is equal to

A particle of mass m is released from point A as shown in the gigure. Would it loop the loop if H=4r? What is the force on the circular track when it is at point (a) B, (b) C?

Figure shows a particle slideing on a frictionles track which terminates in straight horizontal section. If the particle starts slipping from the point. A, how far way from the track will the particle hit the ground ?

A block of mass M with a semi - circular track of radius R rests on a smooth floor. A sphere of mass m and radius r is released from rest from A . Find the velocity of sphere and track , when the sphere reaches B .

Shown a smooth looping the loop track A particle of mass m is released from oint A , as shown If H = 3 r , whould the particle loop the loop ? What is the force on the circular track when the particle is at point (i) B (ii) C ? .

A wedge of mass M is kept at rest on smooth surface a particle of mass m hits the wedge normally. Find the velocity of wedge and particle just after collision. Take coefficient of restitution as e .

A particle of mass m moving with velocity u collides elastically head on with a particle of mass 2m at rest. After collision the heavier particle moves with velocity?

A particle of mass m is suspended from point O and undergoes circular motion in horizontal plane as conical pendulum as shown in figure.