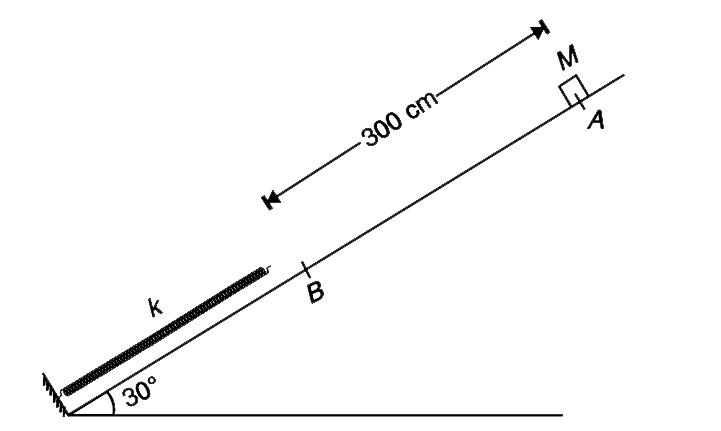
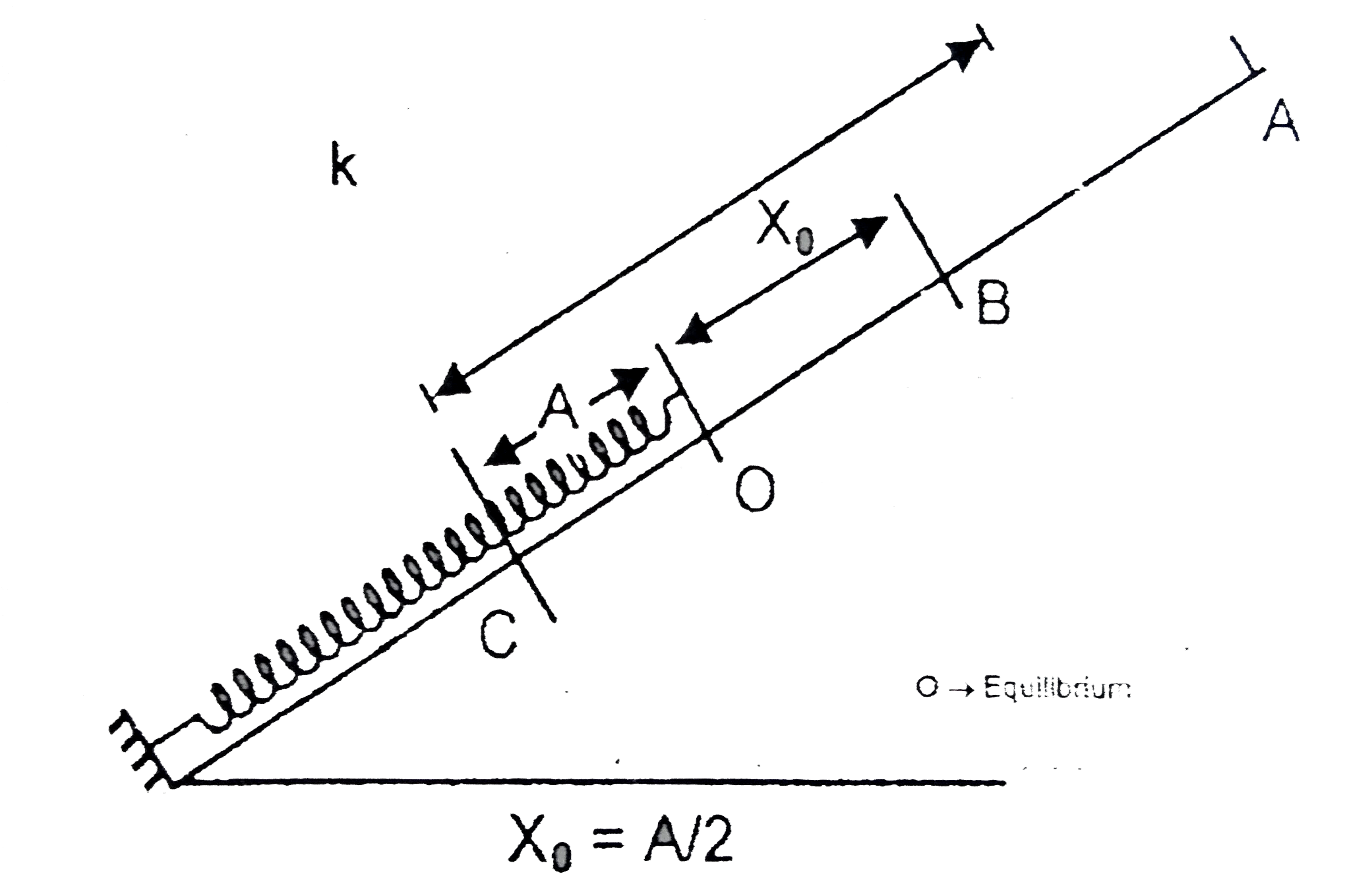
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A block of mass M = 40 kg is released on a smooth incline from point A...
Text Solution
|
- A block of mass m is suddenly released from the top of a spring of sti...
Text Solution
|
- A block of mass m length force a verical of spring constant k If the b...
Text Solution
|
- A block of mass M connected to an ideal spring of force constant k, is...
Text Solution
|
- Two small blocks of mass m and 4m are connected to two springs as show...
Text Solution
|
- A block of mass M = 40 kg is released on a smooth incline from point A...
Text Solution
|
- A block of mass 8 kg is released from the top of an inclined smooth su...
Text Solution
|
- A block of mass 4 kg is released from the top of an inclined smooth su...
Text Solution
|
- A block of mass sqrt2 kg is released from the top of an inclined smoot...
Text Solution
|