A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
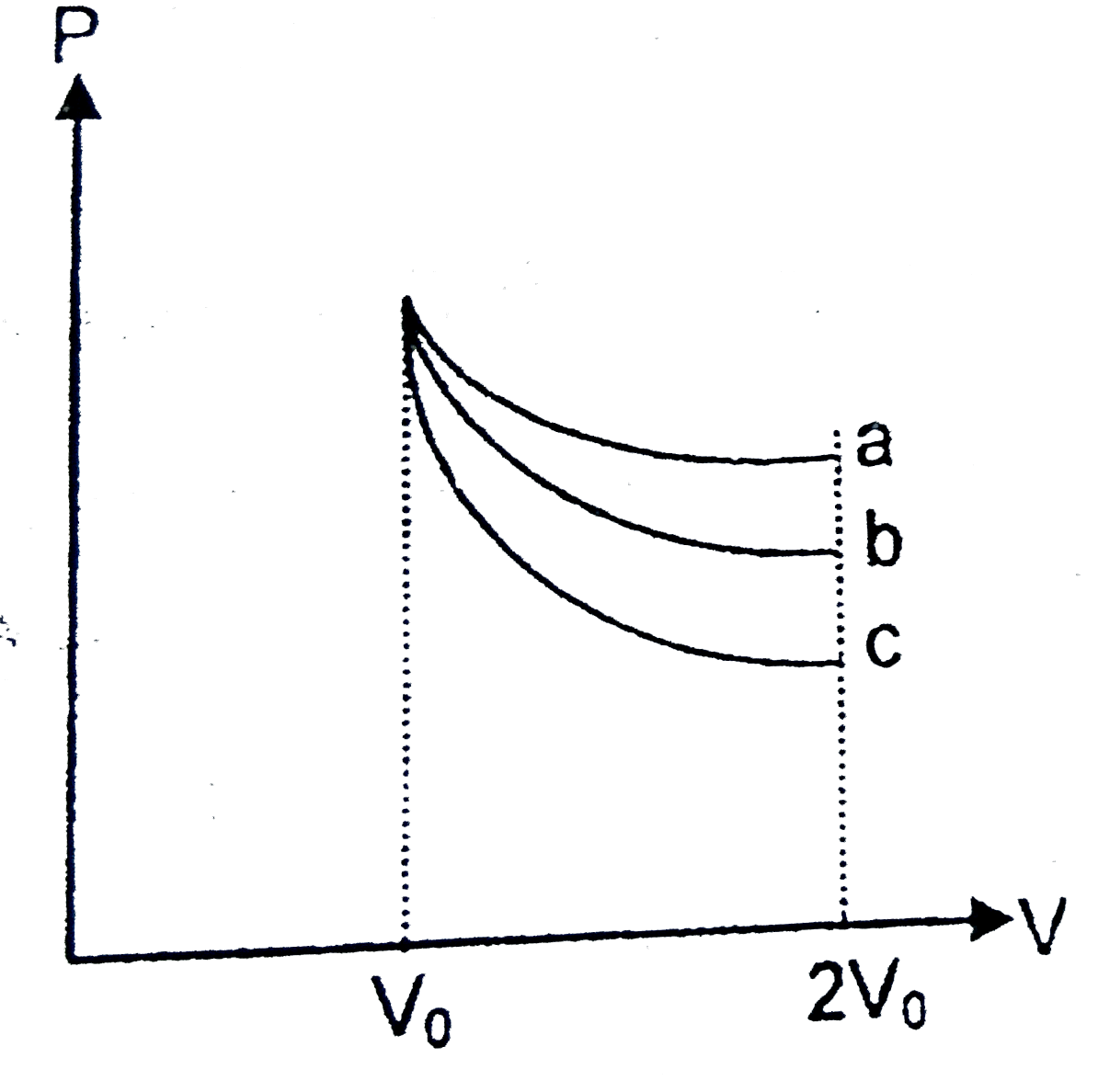
- An ideal gas may expands from V(0) to 2V(0) according to following thr...
Text Solution
|
- An ideal gas may expands from V(0) to 2V(0) according to following thr...
Text Solution
|
- An ideal diatomic gas undergoes a process in which the pressure is pro...
Text Solution
|
- An ideal gas expands according to the laq PV^(3)/(2) = constant. Then ...
Text Solution
|
- An ideal gas expands according to the law pV^(2)= constant (a) Is it h...
Text Solution
|
- The internal energy of a gas is given by U = 3 pV. It expands from V(0...
Text Solution
|
- The internal energy of a gas is given by U= 5 + 2PV . It expands from ...
Text Solution
|
- A gas is expanded form volume V(0) to 2V(0) under three different proc...
Text Solution
|
- An ideal gas whose adiabatic exponent is gamma is expanded according t...
Text Solution
|