Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTRIC CHARGES AND FIELDS
AAKASH INSTITUTE|Exercise TRY YOURSELF|33 VideosELECTRIC CHARGES AND FIELDS
AAKASH INSTITUTE|Exercise ASSIGNMENT(SECTION-A) Objective Type Question|47 VideosDUAL NATURE OF RADIATION AND MATTER
AAKASH INSTITUTE|Exercise ASSIGNMENT (SECTION-D)|10 VideosELECTROMAGNETIC INDUCTION
AAKASH INSTITUTE|Exercise ASSIGNMENT(SECTION -D) Assertion-Reason type Question)|15 Videos
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE-ELECTRIC CHARGES AND FIELDS -SECTION -J(Aakash Challengers Questions)
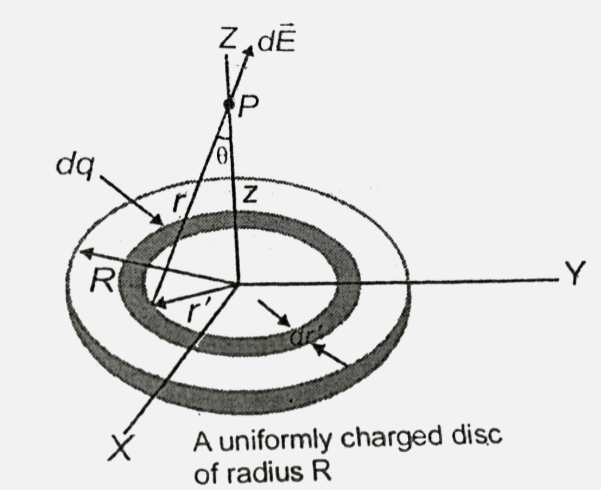
- A uniformly charged disc of radius R with a total charge Q lies in the...
Text Solution
|
- Planes x= 2 and y = -3 , respectively , carry charge densities10 nC //...
Text Solution
|
- The electric field in a region is given as E= (1)/(epsilon(0))[( 2y^...
Text Solution
|
- A particle of mass m carries an electric positive charge Q and is subj...
Text Solution
|
- A metallic sphere of radius R is cut in two parts along a plane whose ...
Text Solution
|
- The distance between the plates of a planar capacitor is d and area of...
Text Solution
|