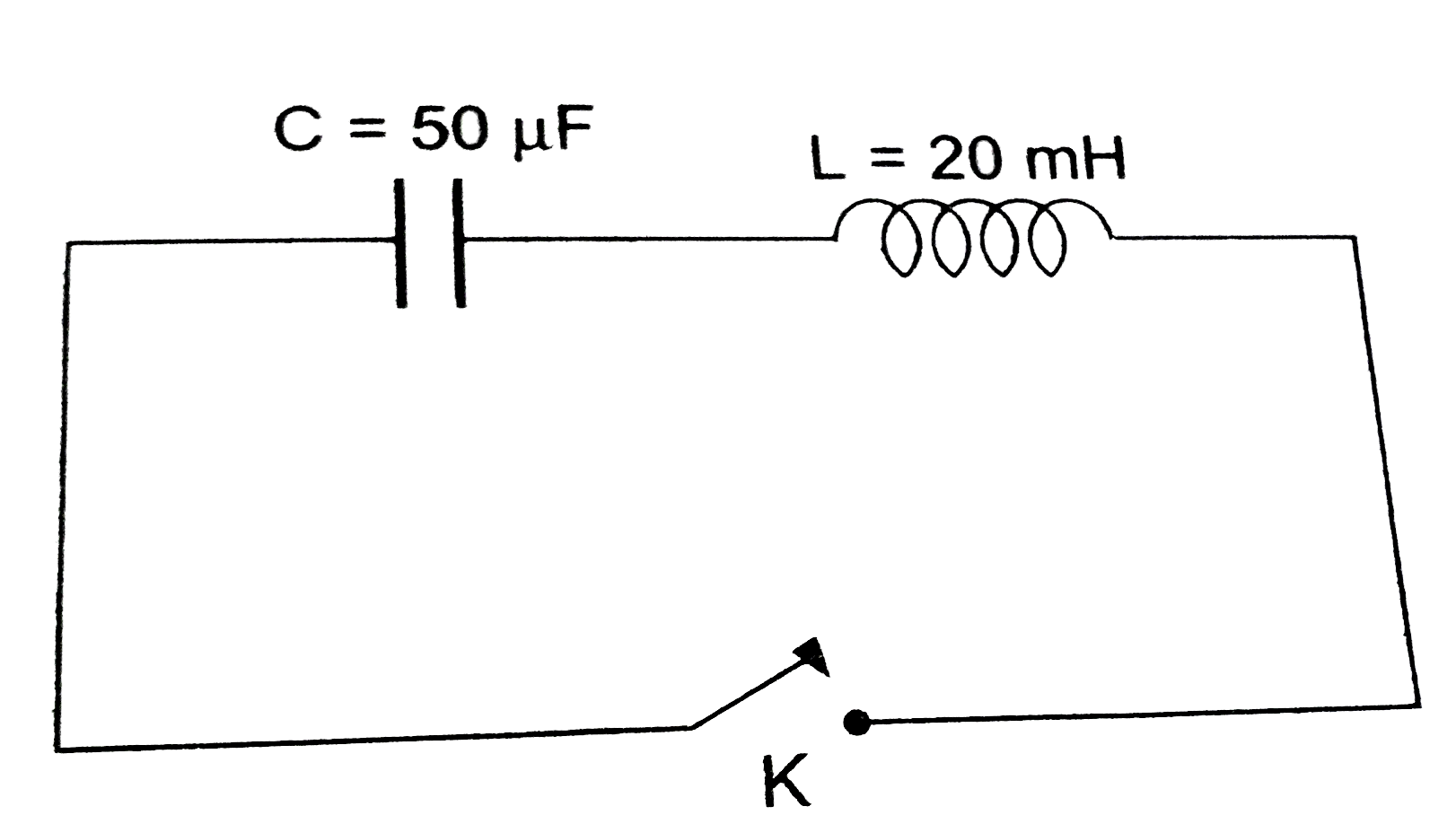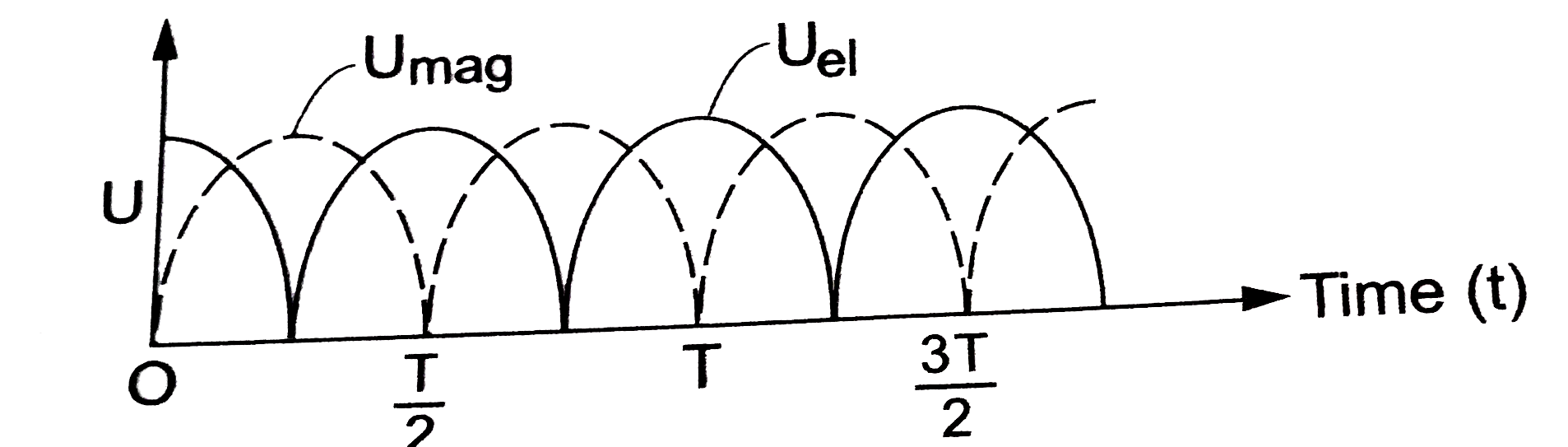प्रश्न से , `L = 20 mH = 20 xx 10^(-3) H, C = 50 mu F = 50 xx 10^(-6) F, R = 0`,
संधारित्र पर प्रारंभिक आवेश `Q_(0) = 10 mC = 10 xx 10^(-3) C`.
(a) प्रारम्भ में परिपथ में धारा शून्य है , अतः सम्पूर्ण विधुत - ऊर्जा संधारित्र में निहित होगी , अर्थात
`U_("Total") =Q_(0)^(2)/(2C) = ((10^(-2)C)^(2))/(2(50 xx 10^(-6)F)) = 100/100 J = 1 J`.
चूँकि परिपथ में प्रतिरोध शून्य है , अतः धारा - प्रवाह के क्रम में ऊष्मा के रूप में ऊर्जा - क्षय नहीं होता है । अतः ,L -C दोलन के क्रम में कुल ऊर्जा संरक्षित (conserved) रहती है ।
(b) L-C परिपथ की स्वाभाविक आवृत्ति ,
`f = 1/(2 pi sqrt(LC)) = 1/(2 xx 3 .14 xx sqrt((20 xx 10^(-3)H)(50 xx 10^(-6)F)))`
`= (10^(4))/(2 xx 3 .14 xx sqrt100)Hz = 159.24 Hz approx 159 Hz`.
(c ) विधुतीय दोलन का आवर्तकाल `T = 1/f = 1/((159 Hz))`
` = 0.0063 s = 6.3 xx 10^(-3) s`.
(i) दोलन के क्रम में विधुतीय एवं चुंबकीय ऊर्जा के बीच आवर्त रूप से परस्पर विनिमय (exchange) होता रहता है , जो चित्र 2.5-3 के अनुसार होता है ।
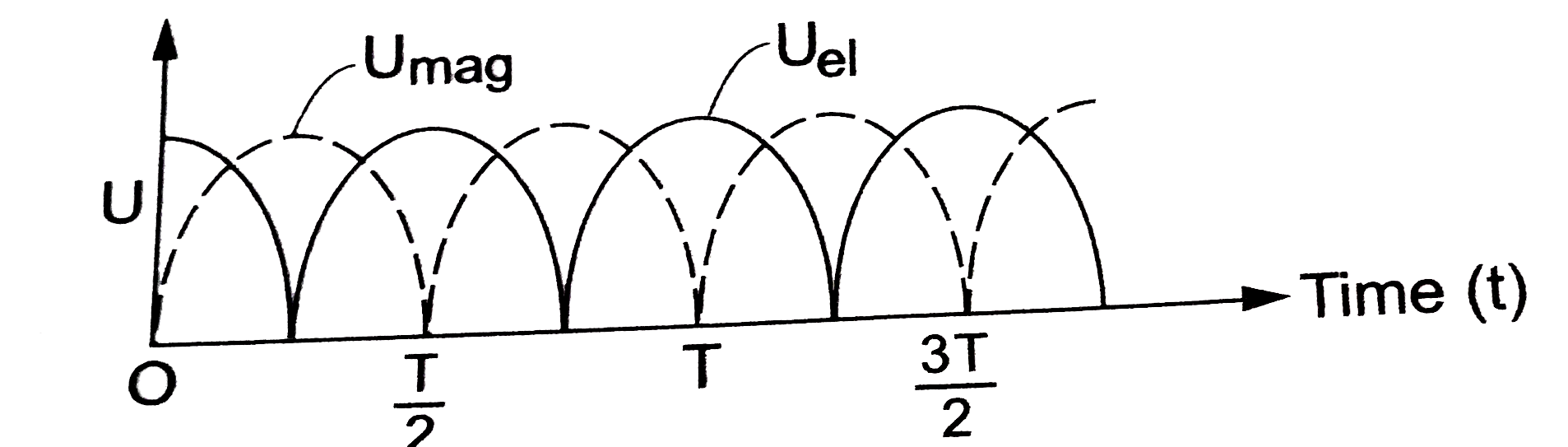
परिपथ में ऊर्जा पूर्णतः विधुतीय ( संधारित्र पर ) होती है जब समय `t = 0, T/2 , T, (3T)/2, ..., ` जहाँ `T = 6.3 `m s.
(ii)परिपथ में ऊर्जा पूर्णतः चुंबकीय ( प्रेरित्र पर ) होती है जब समय `t = T/4, (3T)/4, (5T)/4 ,...,`जहाँ `T = 6.3 ` ms.
(d) परिपथ की कुल ऊर्जा ,`U_("Total")=(Q^(2)/(2C))_("max") = Q_(0)^(2)/(2C)`
विधुत - ऊर्जा का मान होने पर संधारित्र पर आवेश ,
` Q = pm Q_(0)/sqrt2` ...(1)
अब परिपथ में संधारित्र पर तात्कालिक आवेश ,
` Q = Q_(0) cos omega t` ....(2)
समीकरण (1) तथा (2) से ,
`Q_(0) cos omegat = pm Q_(0)/sqrt2`
या `cos omega t= pm 1/sqrt2`
या `omegat = pi/4, (3pi)/4, (5pi)/4, (7pi)/4, ...`
या `t = T/8, (3T)/8, (5T)/8, (7T)/8,..., `जहाँ T = `6.3` m s.
समय के इन मोनों पर परिपथ की कुल ऊर्जा का आधा - आधा भाग संधारित्र एवं प्रेरित्र से संबंध होगा ।
(e) प्रतिरोधक की उपस्थिति में ऊर्जा का क्षय जूल में होता रहेगा । दोलन का यह रूप मुक्त - अवमंदित दोलन (free- damped oscillation) जैसा होगा तथा संपूर्ण ऊर्जा अंततः ऊष्मा में बदल जाएगी तथा विधुतीय समाप्त हो जाएगा ।