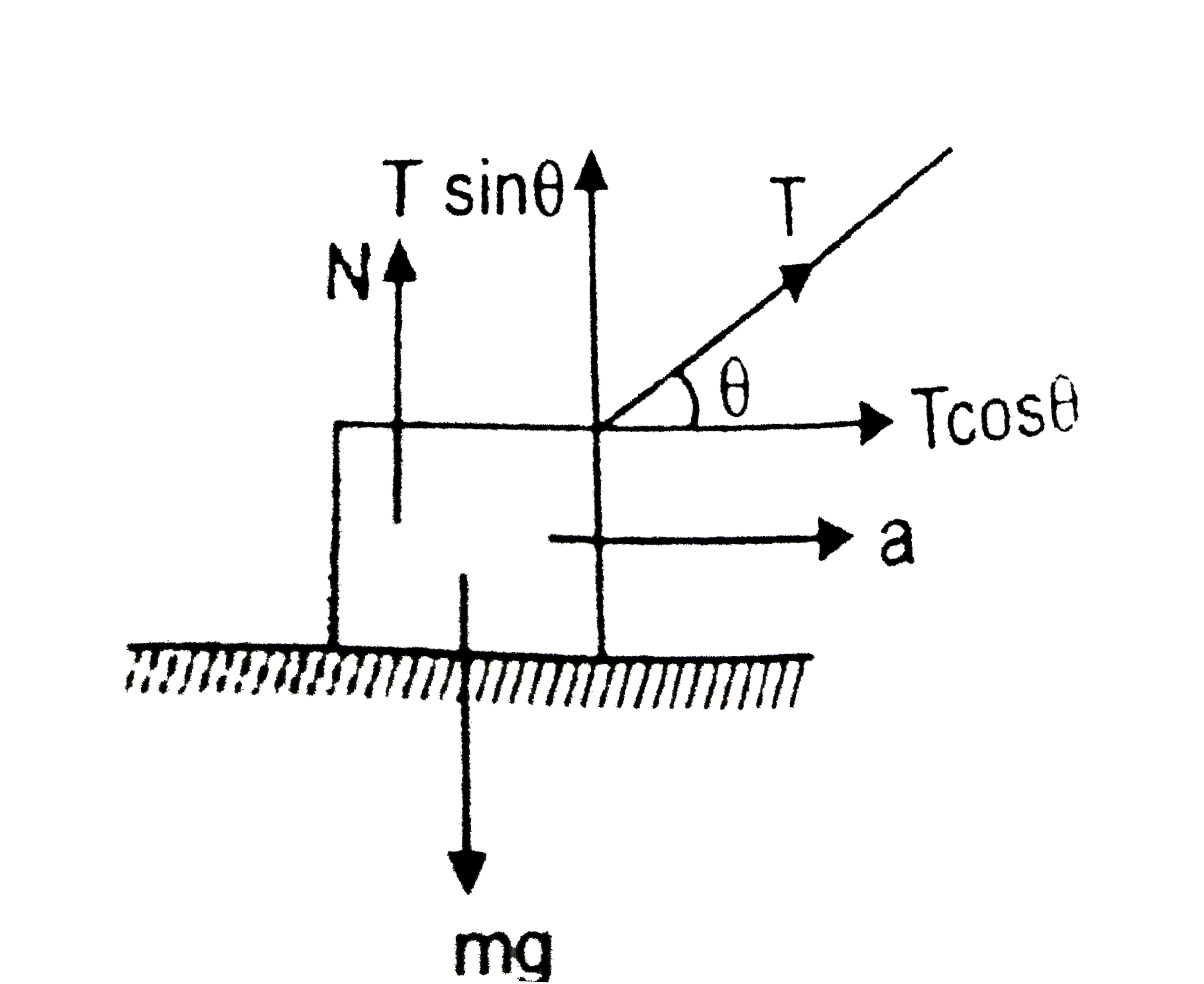Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 30|4 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise Comprehension|127 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 28|7 VideosCURRENT ELECTRICITY
RESONANCE|Exercise Exercise|54 VideosELASTICITY AND VISCOCITY
RESONANCE|Exercise Advanced Level Problems|9 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEMS-dpp29
- A particle of mass 5kg is moving on rough fixed inclined plane with co...
Text Solution
|
- A block A of mass 4 kg is kept on ground. The coefficient of friction ...
Text Solution
|
- If the coefficient of friction between A and B is mu, the maximum acce...
Text Solution
|
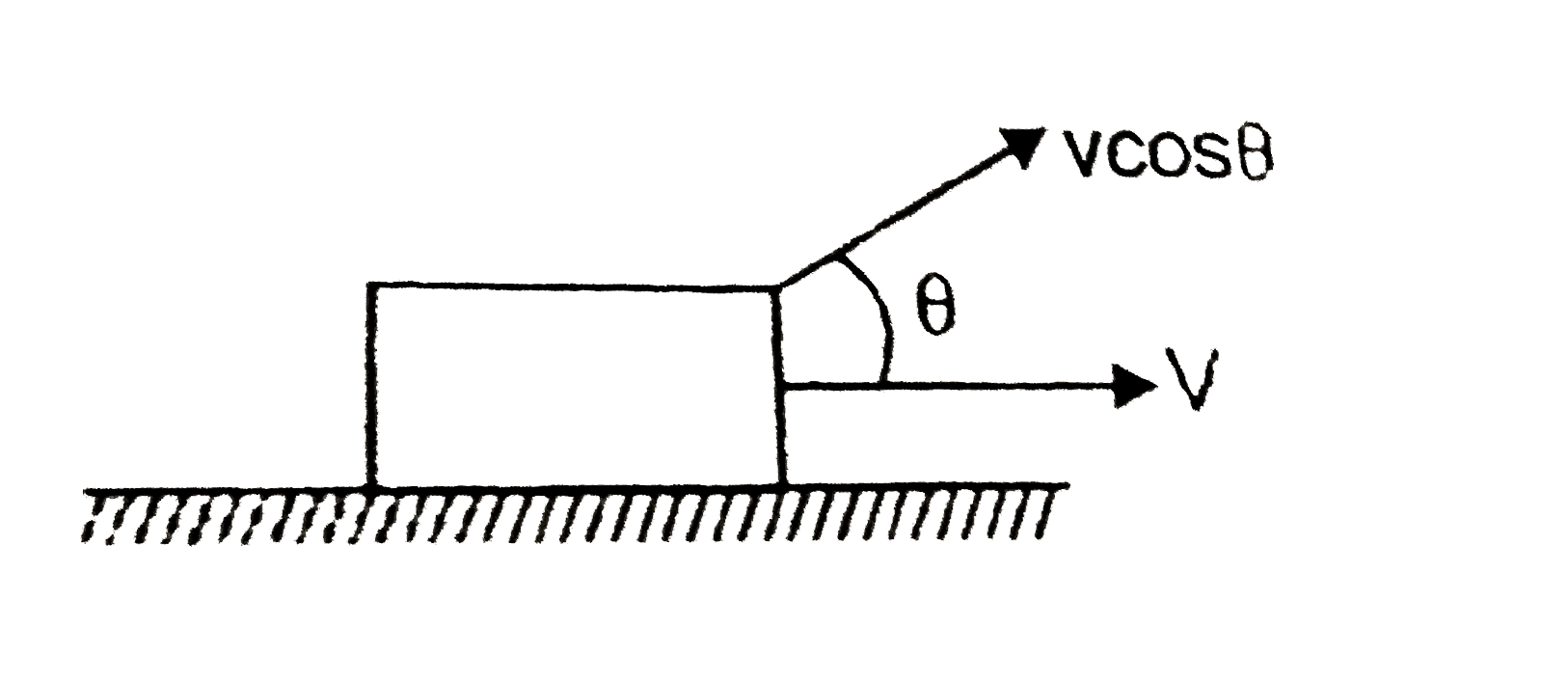
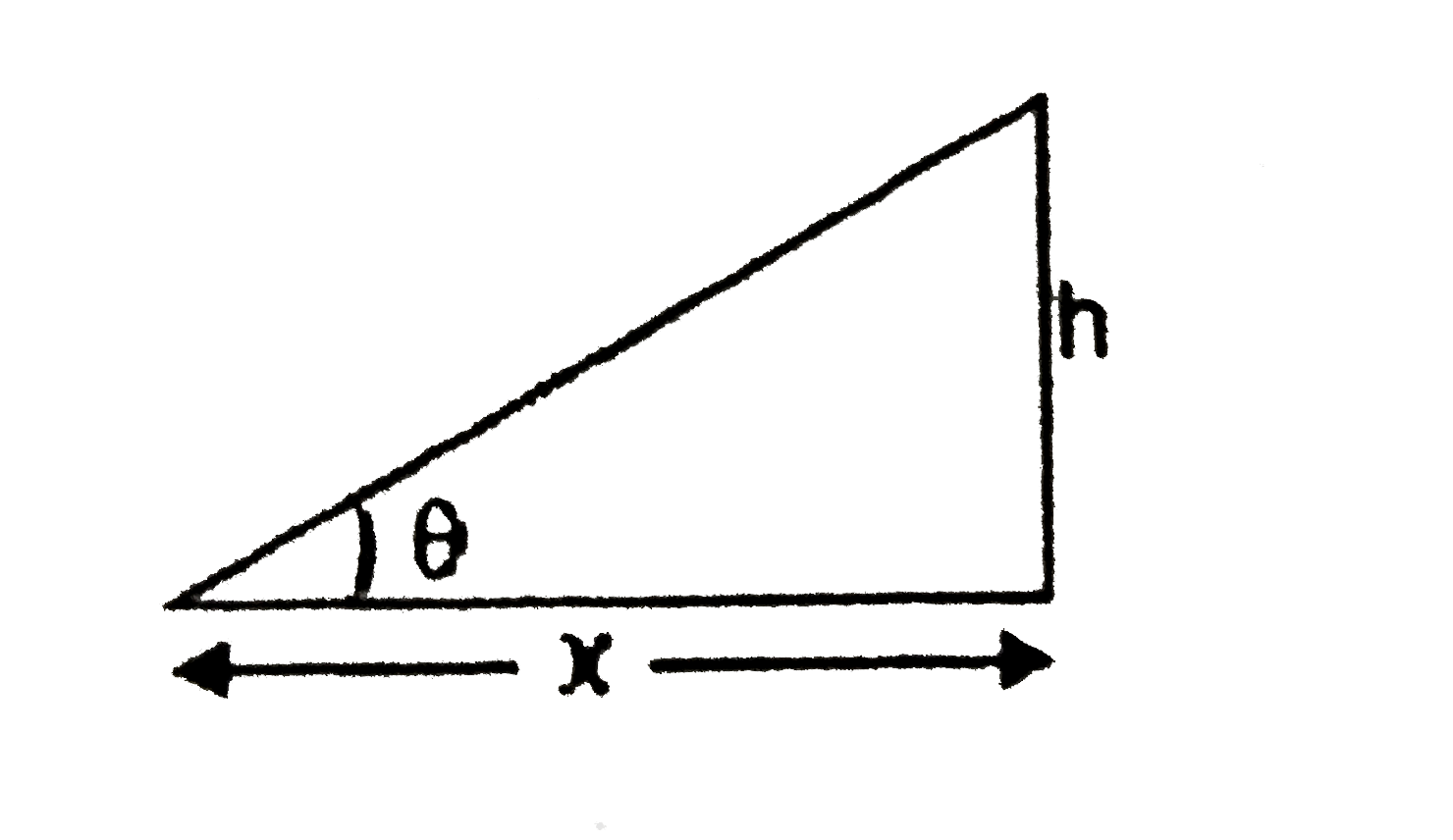
- In the figure shown, a person pulls a light string with a constant spe...
Text Solution
|
- Answer the following briefly. ( Answer should not be of more than one ...
Text Solution
|