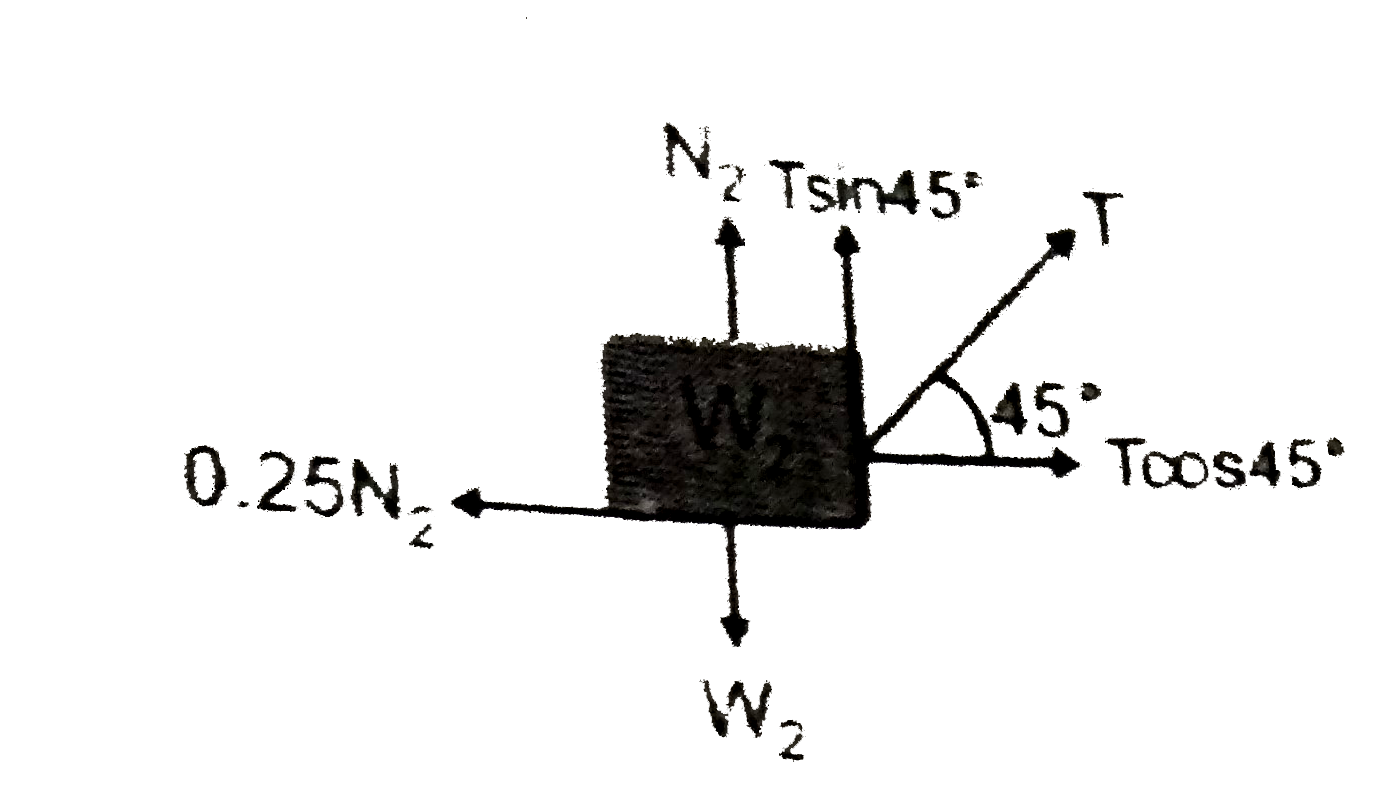A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 34|5 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise DPP 35|5 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 32|8 VideosCURRENT ELECTRICITY
RESONANCE|Exercise Exercise|54 VideosELASTICITY AND VISCOCITY
RESONANCE|Exercise Advanced Level Problems|9 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEMS-dpp 33
- Two stones are projected simultaneously from a tower a differenct angl...
Text Solution
|
- A box is placed on an inclined plane and has to be pushed down.The ang...
Text Solution
|
- A block of mass 20 kg is acted upon by a force F=30N at an angle 53^@ ...
Text Solution
|
- Two blocks of masses 5 kg and 3 kg are placed in contact over an incli...
Text Solution
|
- A block A (5kg) rests over another block B (3kg) placed over a smooth ...
Text Solution
|
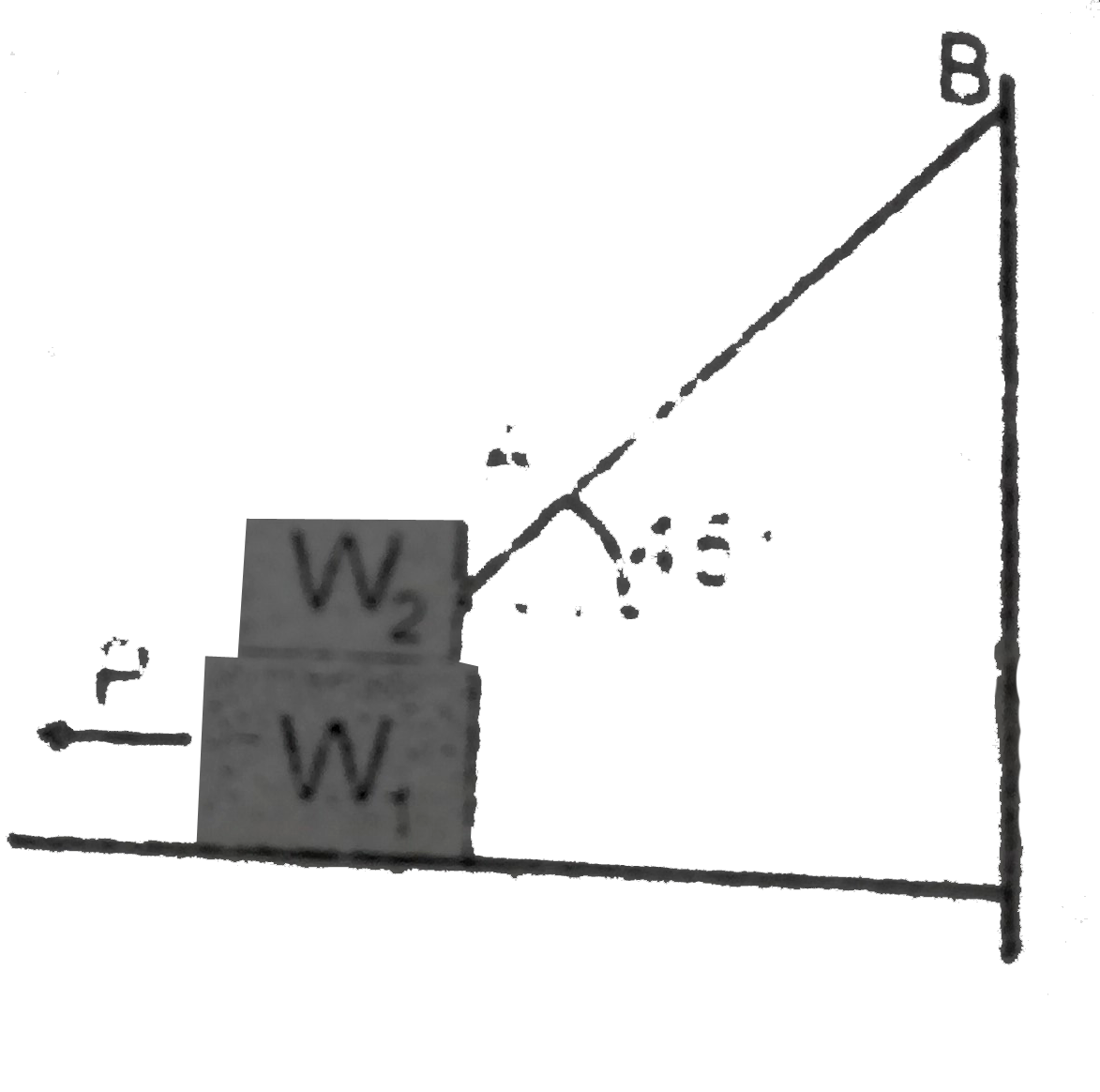
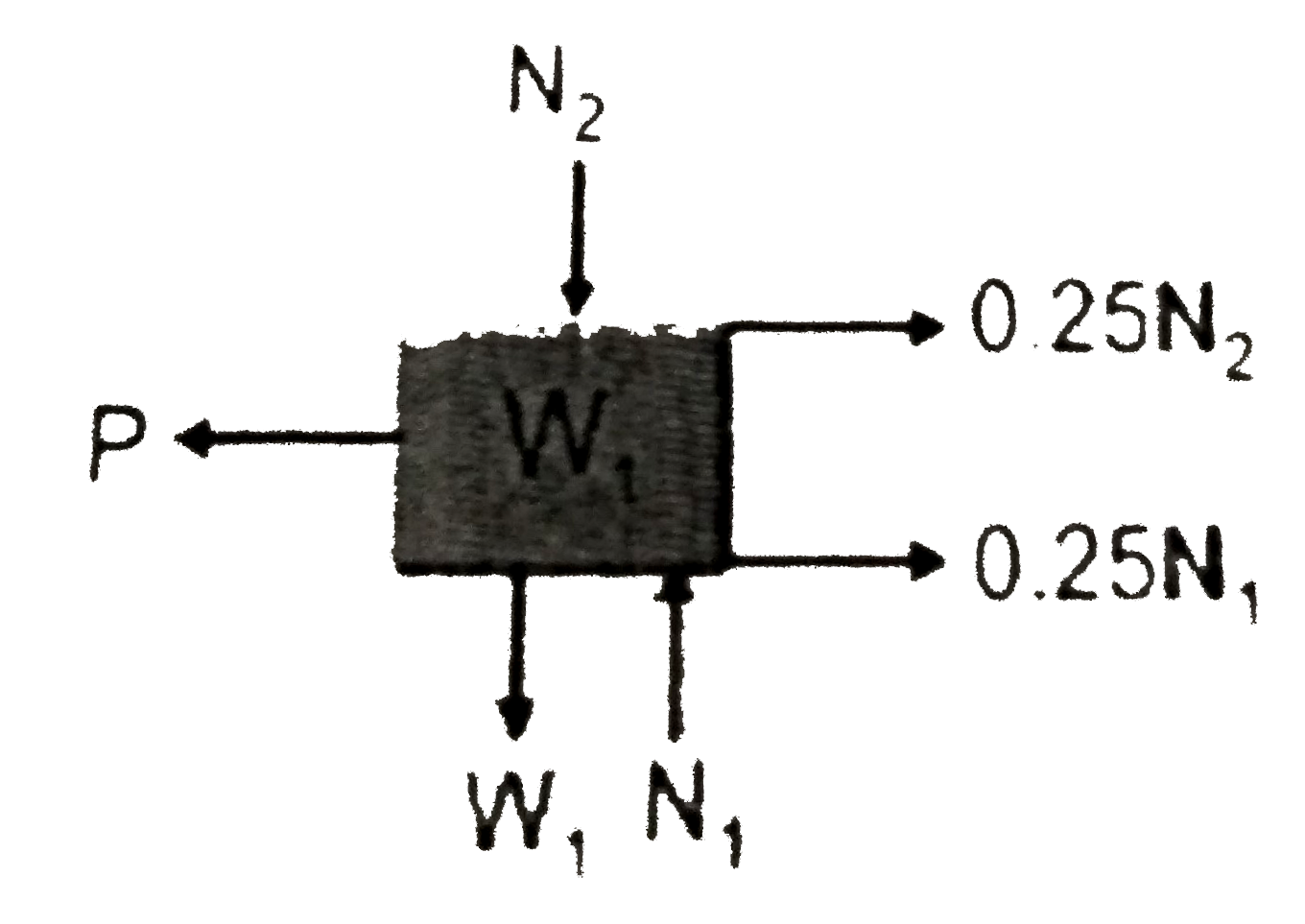
- In the arrangement shown, W(1) = 200N, W(2) = 100 N,mu = 0.25 for all ...
Text Solution
|
- Figure shows a small block A of mass m kept at the left end of a plank...
Text Solution
|
- Find the tensions in the string (1),(2) and (3) and the acceleration o...
Text Solution
|