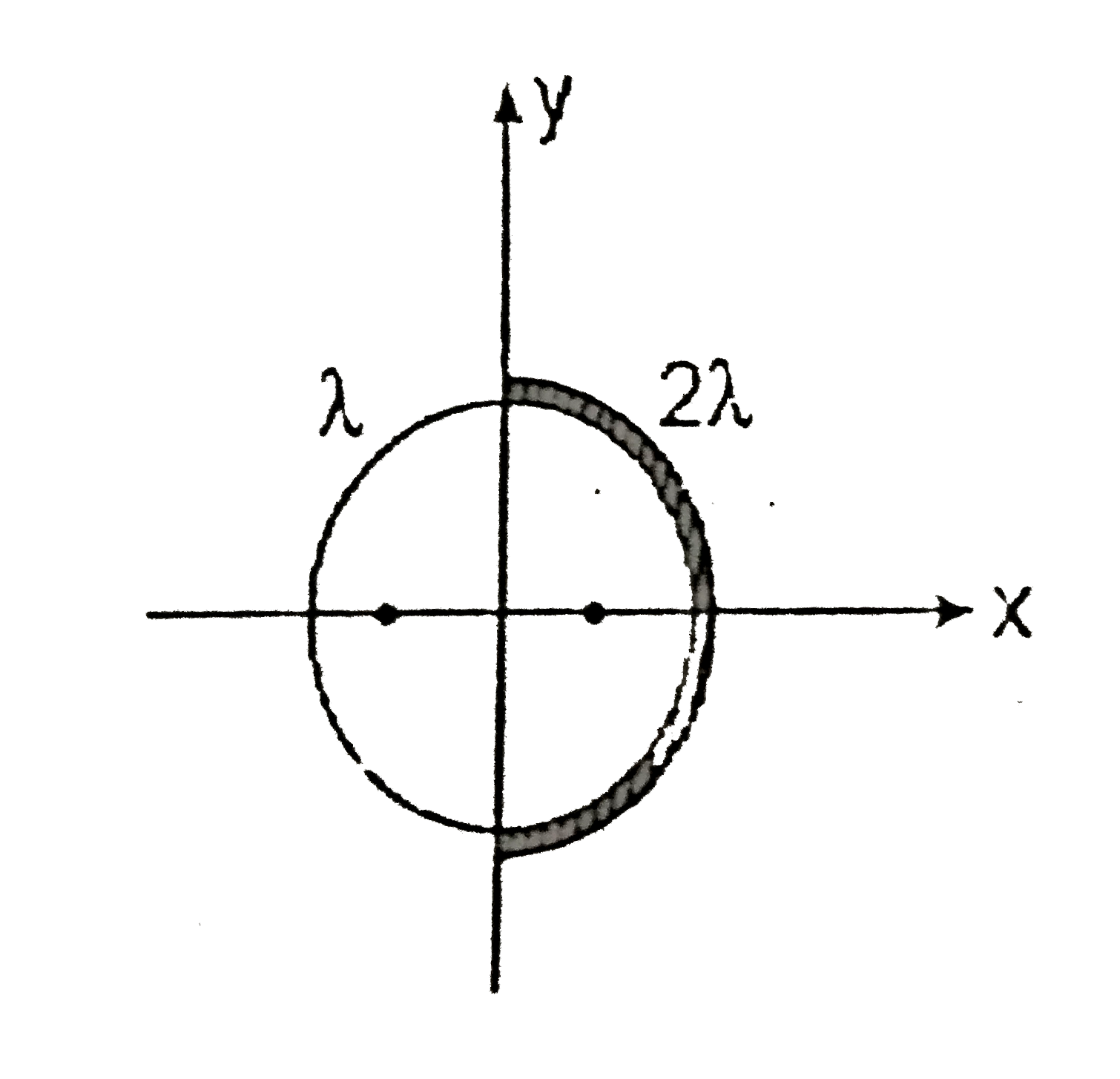A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 46|6 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 47|7 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 44|5 VideosCURRENT ELECTRICITY
RESONANCE|Exercise Exercise|54 VideosELASTICITY AND VISCOCITY
RESONANCE|Exercise Advanced Level Problems|9 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEMS-DPP 45
- A circular curve of a highway is designed for traffic moving at 72km//...
Text Solution
|
- Two semicircular rings of linear mass densities lamda and 2 lamda and ...
Text Solution
|
- The centre of mass of a non uniform rod of length L, whose mass per un...
Text Solution
|
- A bead of mass m is located on a parabolic wire with its axis vertical...
Text Solution
|
- A uniform thin rod is bent in the form of closed loop ABCDEFA as shown...
Text Solution
|
- A particle of mass m is fixed to one end of a massless spring of sprin...
Text Solution
|
- A body of mass m was slowly hauled up the hill (figure) by a force F w...
Text Solution
|