Home
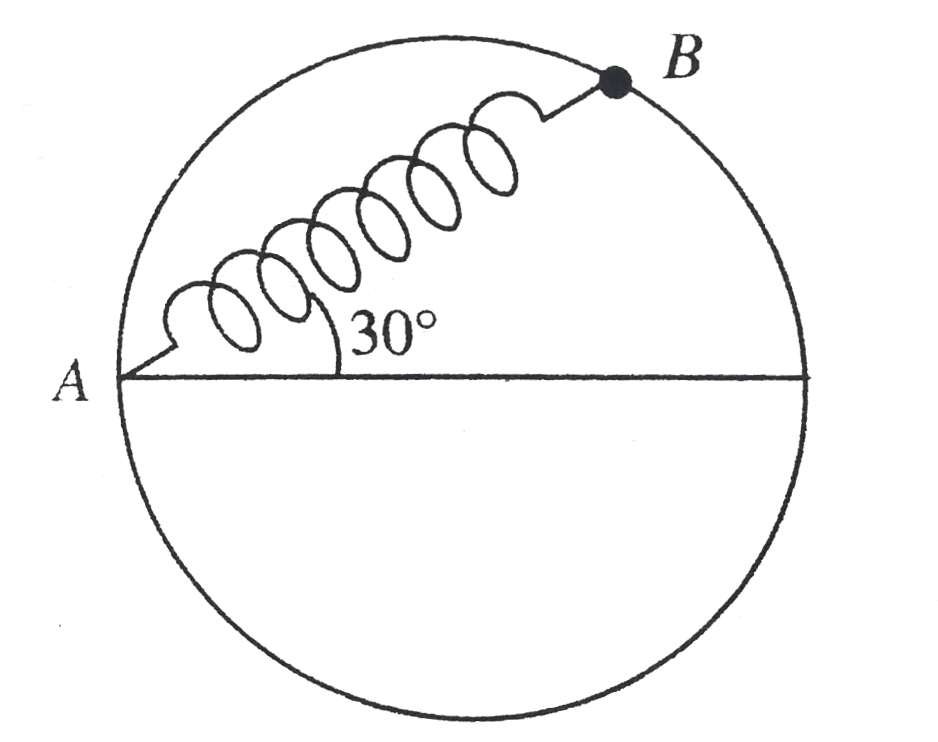
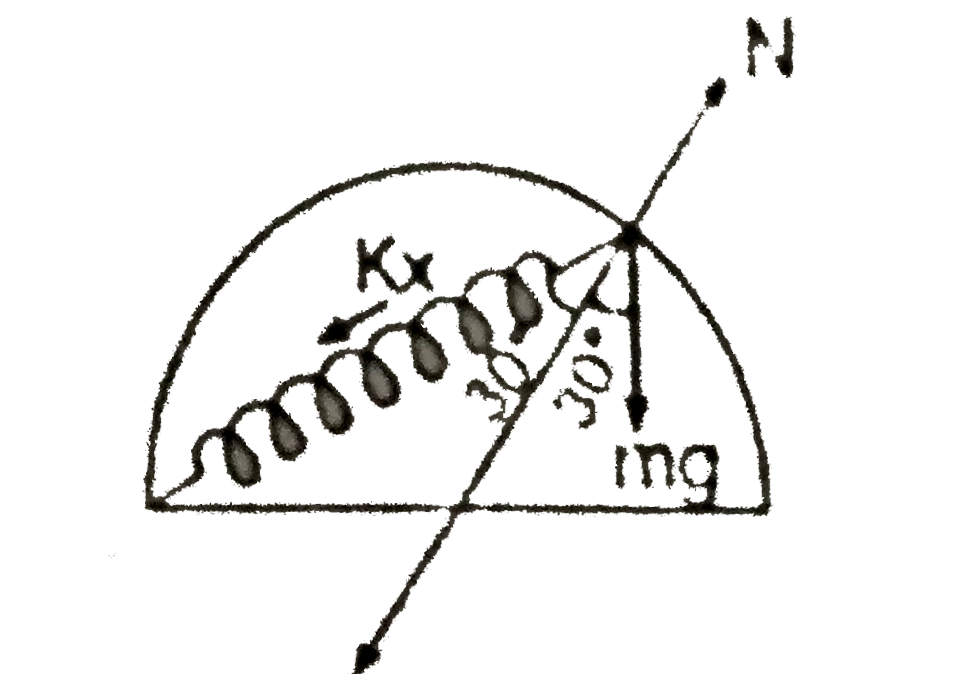
Class 11
PHYSICS
A bead of mass m is attached to one end ...

A bead of mass m is attached to one end of a spring of natural length R and spring constant `K=((sqrt(3)+1)mg)/(R )`. The other end of the spring is fixed at a point A on a smooth vertical ring of radius R as shown in fig. The normal reaction at B just after it is released to move is

A

`(mg)/(2)`

B

`sqrt(3)mg`

C

`3sqrt(3)mg`

D

`(3sqrt(3)mg)/(2)`

Text Solution

Verified by Experts

The correct Answer is:
D
The extension is spring is `x=2R cos 30^(@)-R=(sqrt(3)-1)R`

`kx cos 30^(@)+mg cos 30^(@)`
Applying Newton's second law to the bead normal to circular rind at point `B`
`N=K(sqrt(3)-1)R cos 30^(@)+mg cos 30^(@)`
`=((sqrt(3)-1))/(R) mg (sqrt(3)-1)R cos 30^(@)+mg cos 30^(@)`
`N=(3 sqrt(3)mg)/(2)`.
Promotional Banner

Topper's Solved these Questions

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 48|4 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 49|6 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 46|6 Videos

  • CURRENT ELECTRICITY

    RESONANCE|Exercise Exercise|54 Videos

  • ELASTICITY AND VISCOCITY

    RESONANCE|Exercise Advanced Level Problems|9 Videos

Similar Questions

Explore conceptually related problems

A Bead of mass m is attached to one end of a spring of natural length 'R' and spring cosntant 'k=((sqrt3+1)mg)/R' . The other end of the spring is fixed at point 'A' on a smooth vertical ring of radius 'R' as shown

A bead of mass 'm' is attached to one end of a spring of natural length R & spring constant k = ((sqrt3 + 1))/(R) . The other end of the spring is fixed at point A on a smooth vertical ring of radius R as shown. The normal reaction at B just after it is released to move is

A block of mass 'm' is attached to a spring in natural length of spring constant 'k' . The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.

A bead of mass m can slide without friction on a fixed circular horizontal ring of radius 3R having a centre at the point C. The bead is attached to one of the ends of spring of spring constant k. Natural length of spring is R and the other end of the spring is R and the other end of the spring is fixed at point O as shown in the figure. If the bead is released from position A, then the kinetic energy of the bead when it reaches point B is

A ring of mass m is attached to a horizontal spring of spring constant k and natural length l_0 . The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.

A block ofmass m is attached with a spring in its natural length, of spring constant k. The other end A of spring is moved with a constant acceleration 'a' away from the block as shown in the figure -3.74 . Find the maximum extension in the spring. Assume that initially block and spring is at rest w.r.t ground frame:

A small block of mass m, can move without friction on the outside of a fixed vertical circular track of radiusR. The block is attached to a spring of natural length R//2 and spring constant K. The other end of spring is connected to a point at height R//2 directly above the centre of track. If the block is released from rest when the spring is in horizontal state (see figure) then at that moment,

A small block of mass m, can move without friction on the outside of a fixed vertical circular track of radiusR. The block is attached to a spring of natural length R//2 and spring constant K. The other end of spring is connected to a point at height R//2 directly above the centre of track. If the complete stup is in a gravity free space, then the minimum speed (v_(0)) required at the highest point A to just reach the lowest point is

A small block of mass m, can move without friction on the outside of a fixed vertical circular track of radiusR. The block is attached to a spring of natural length R//2 and spring constant K. The other end of spring is connected to a point at height R//2 directly above the centre of track. Consider block to be at rest at top most point A of track. If the block is slowly pushed from rest at the highest A. When the spring reaches in horizontal state, then.

A block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is mu then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .