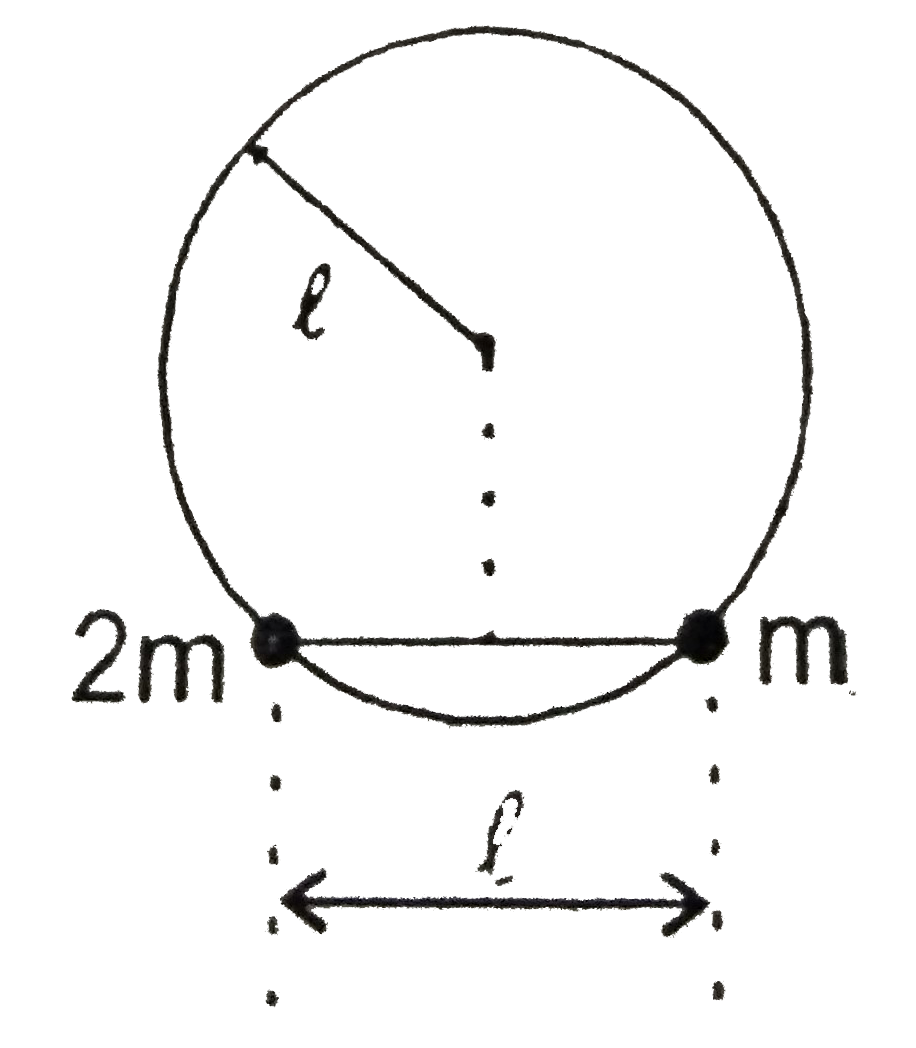
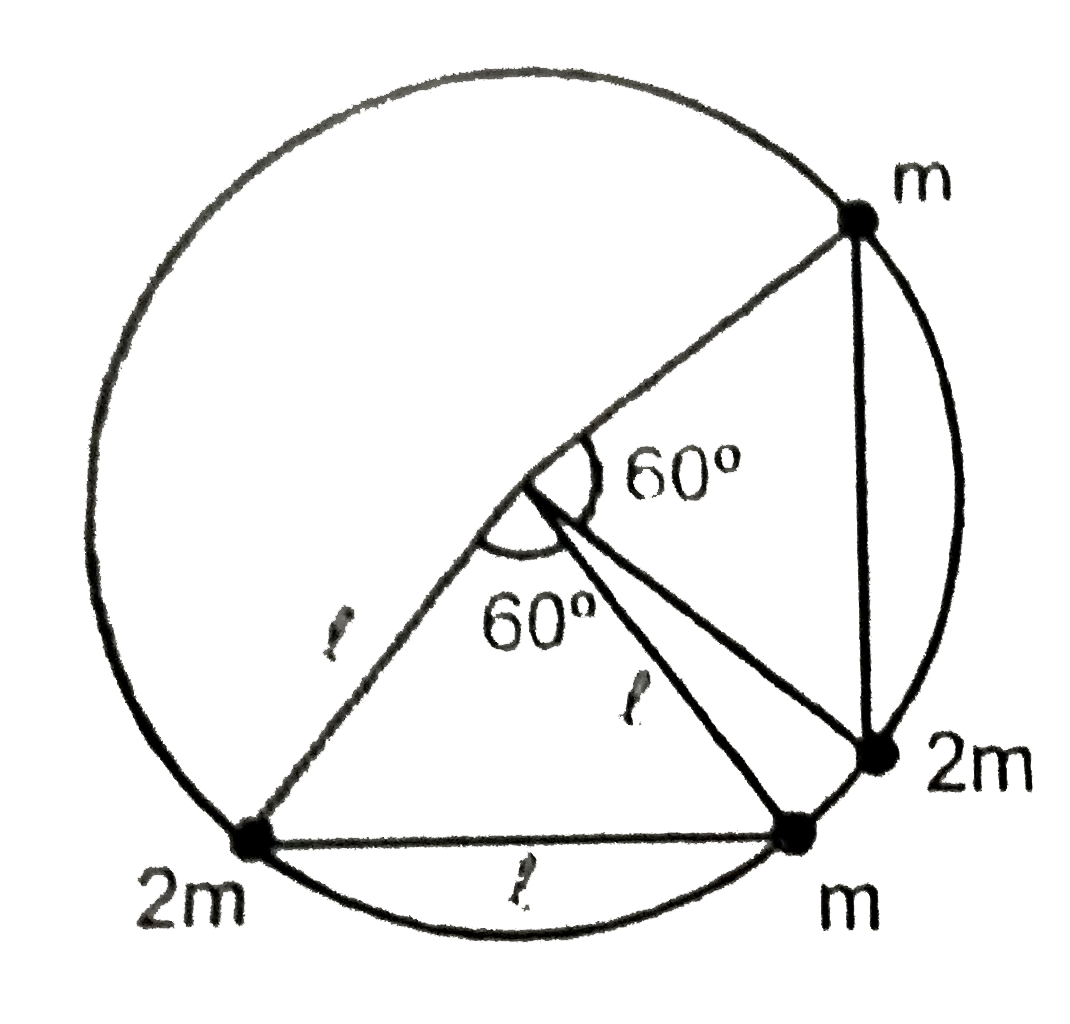
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two beads of mass 2m and m, connected by a rod of length l and of negl...
Text Solution
|
- Two point masses m are connected the light rod of length l and it is f...
Text Solution
|
- A unifrom rod of length l and mass m is free to rotate in a vertical p...
Text Solution
|
- A long rod ABC of mass "m" and length "L" has two particles of masses ...
Text Solution
|
- Two beads of mass 2m and m, connected by a rod of length l and of negl...
Text Solution
|
- Two beads of mass 2m and m , connected by a rod of length l and of neg...
Text Solution
|
- Two beads of mass 2m and m , connected by a rod of length l and of neg...
Text Solution
|
- A uniform rod of length l and mass 2m rests on a smooth horizontal tab...
Text Solution
|
- A rod of mass m and length l is held vertically on a smooth horizontal...
Text Solution
|