Home
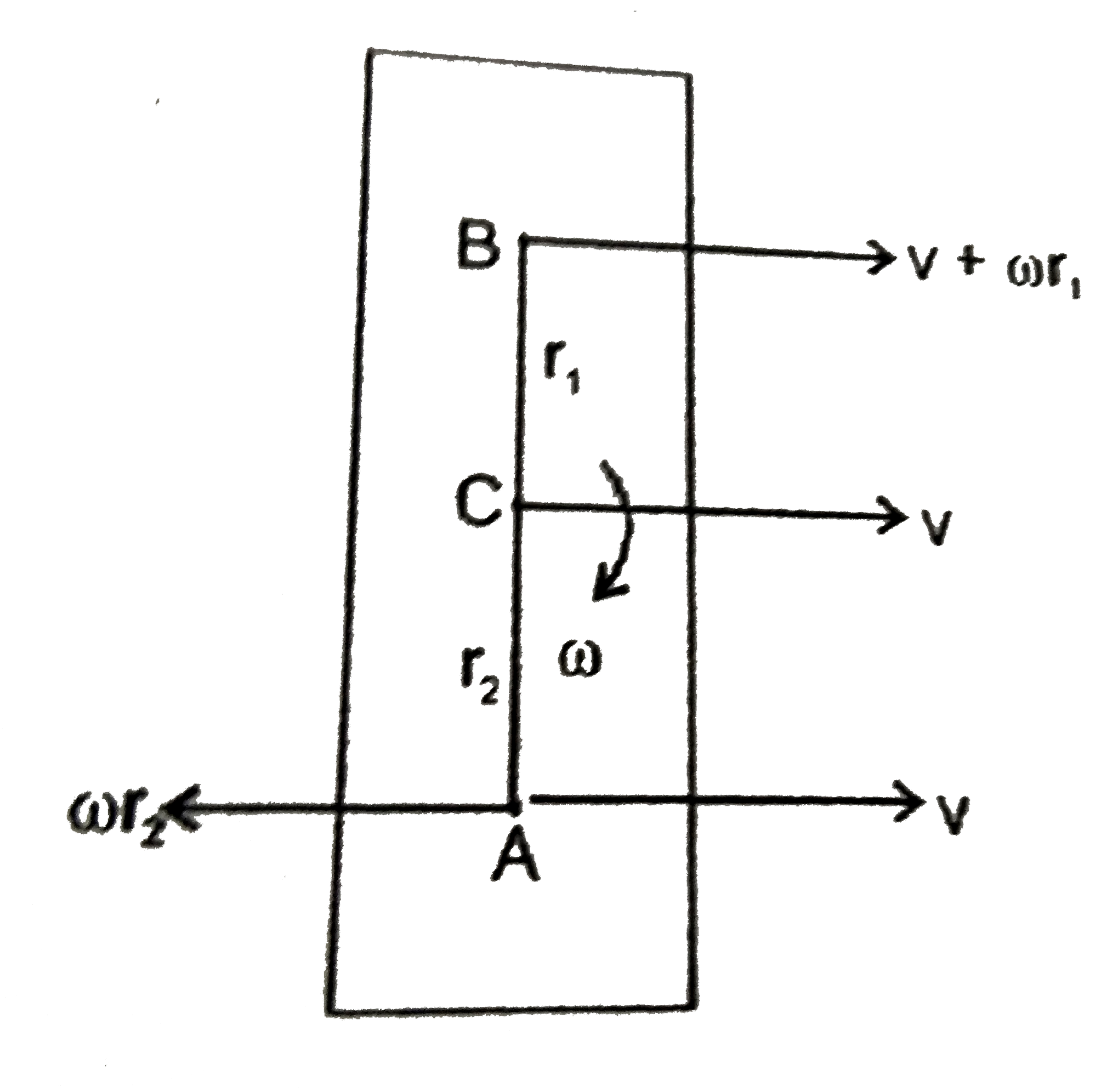
Class 11
PHYSICS
The angular velocity of a rigid body abo...

The angular velocity of a rigid body about any point of that body is same :

A

only in magnitude

B

only in direction

C

both in magnitude and direction necessarily

D

both in magnitude and direction about some points but not about all points.

Text Solution

Verified by Experts

The correct Answer is:
C
Suppose a rod is having angular velocity `omega` about point `C`.

Choose two points `A` and `B` as shown in the figure. Velocity of `B w.r.t.A =(v+omega r_(1))-(v-omegar_(2))`
`=V_(BA)=omega(r_(1)+r_(2))`
Angular velocity of `B w.r.t.A =(v_(BA))/(AB)`
`=(omega(r_(1)+r_(2)))/(r_(1)+r_(2))=omega Ans (C )`
Promotional Banner

Topper's Solved these Questions

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise DPP 62|4 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 63|5 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 60|5 Videos

  • CURRENT ELECTRICITY

    RESONANCE|Exercise Exercise|54 Videos

  • ELASTICITY AND VISCOCITY

    RESONANCE|Exercise Advanced Level Problems|9 Videos

Similar Questions

Explore conceptually related problems

The angular momentum of a rigid body is

Assertion : The angular velocity of a rigid body in motion is defined for the whole body Reason : All points on a rigid body performing pure rotational motion are having same angular velocity.

A : When a rigid body rotates about any fixed axis, then all the particles of it move in circles of different radii but with same angular velocity. R : In rigid body relative position of particles are fixed.

The angular velocity of a rigid body is 24 rad s^(-1) , Calculate the time it will take to rotate 72 rad.

If the angular velocity of a rotating rigid body is increased then its moment of inertia about that axis

Consider a rigid body rotating in a plane. We wish to determine the angular velocity of the rigid body given the known velocities of points A and B on the rigid body. These velocities are parallel and pointing in the same direction. The line joining points A and B is perpendicular to the direction of the velocities. The figure below illustrates the set up of the problem. Note that lC is the intersection of the line passing through points A and B, and the line joining the tip of the vectors v_(A) and v_(B)

A body of moment of inertia about its axis of rotation is 3 kg m^(2) and angular velocity 3 rad/s. The kinetic energy of rotating body is same as that of body of mass 27 kg moving with a speed of

Consider the following two statements A and B and identify the correct choice A) When a rigid body is rotating about its own axis, at a given instant all particles of body posses same angular velocity. B) When a rigid body is rotating about its own axis, the linear velocity of a particle is directly proportional to its perpendicular distance from axis