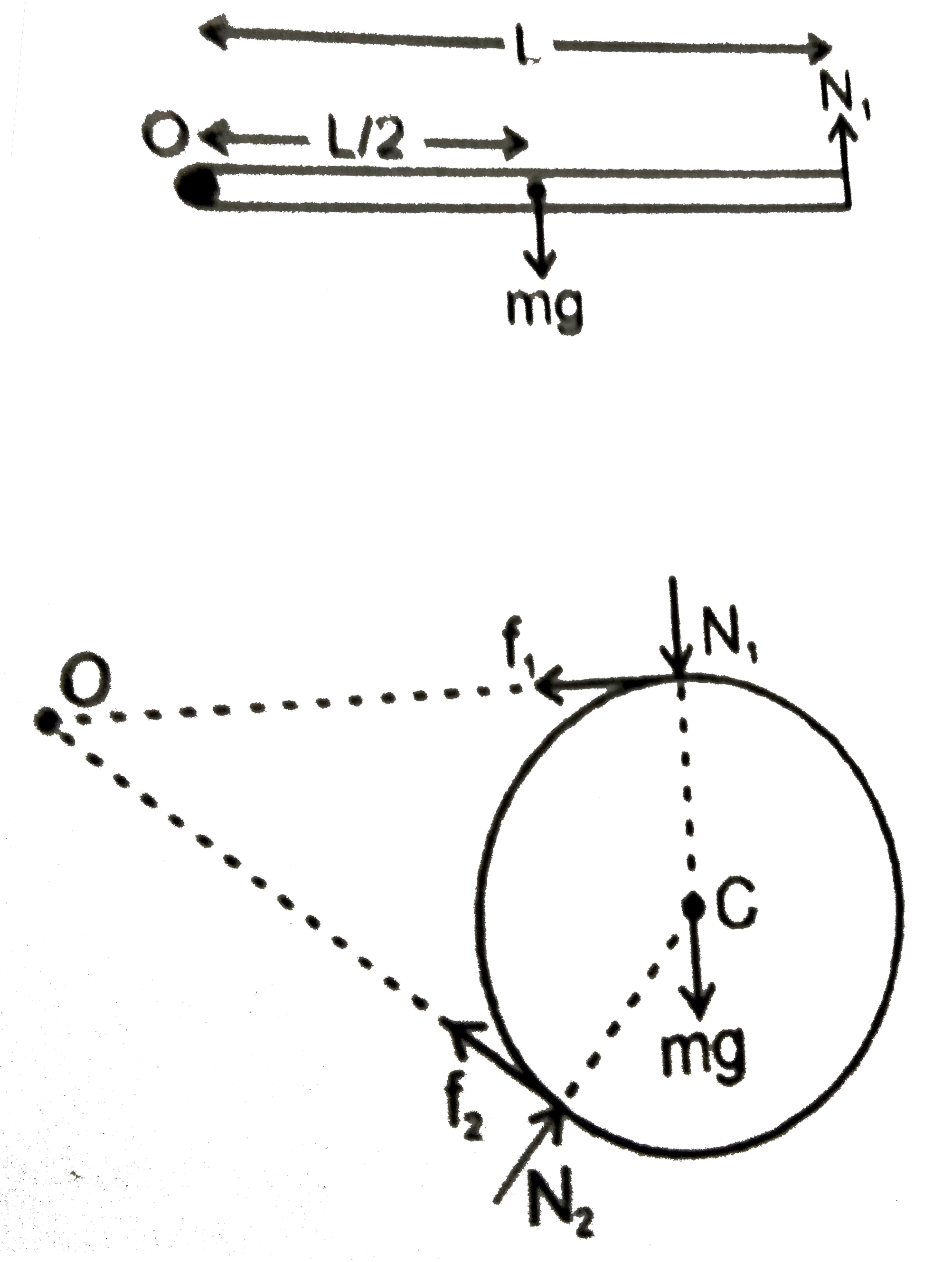
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A horizontal uniform rod of mass 'm' has its left end hinged to the fi...
Text Solution
|
- A uniform cylinder of mass m lies on a fixed plane inclined at a angle...
Text Solution
|
- A solid cylinder of mass m and radius r is rolling on a rough inclined...
Text Solution
|
- A solid cylinder of mass m rolls without slipping down an inclined pla...
Text Solution
|
- A horizontal uniform rod of mass 'm' has its left end hinged to the fi...
Text Solution
|
- A horizontal uniform rod of mass 'm' has its left end hinged to the fi...
Text Solution
|
- A horizontal uniform rod of mass 'm' has its left end hinged to the fi...
Text Solution
|
- A horizontal stick of mass m has its right end attached to a pivot on ...
Text Solution
|
- A solid cylinder of mass 8 kg is rolling perfectly down an inclined pl...
Text Solution
|