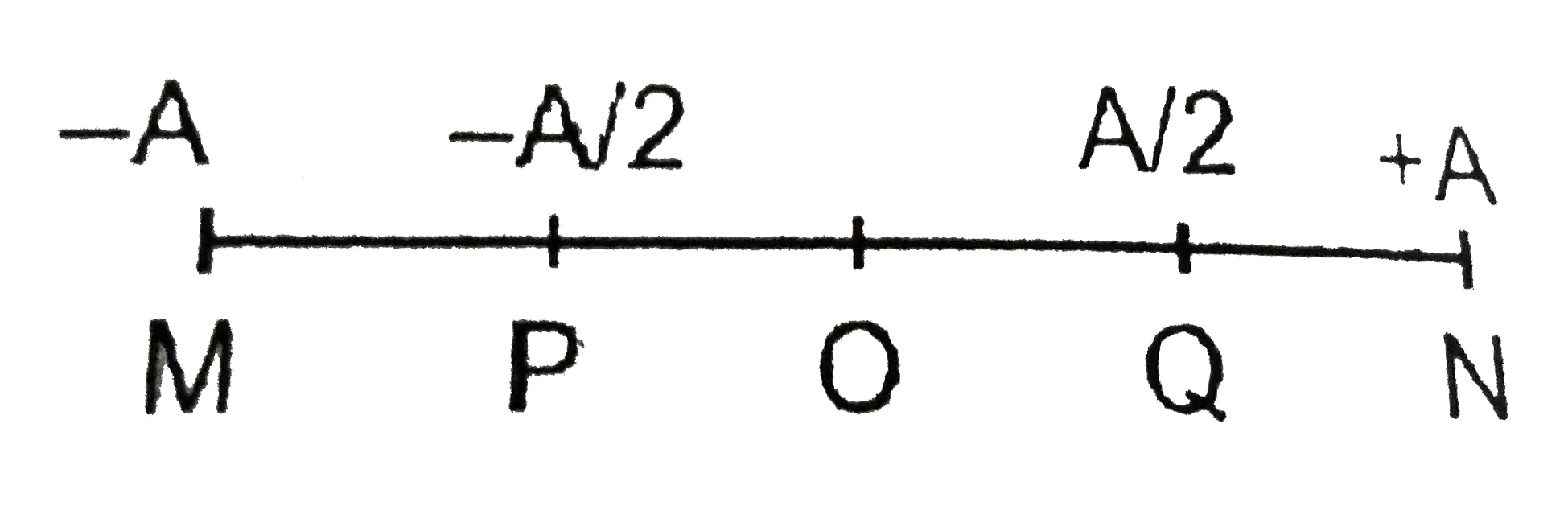A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 71|8 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 72|4 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 69|5 VideosCURRENT ELECTRICITY
RESONANCE|Exercise Exercise|54 VideosELASTICITY AND VISCOCITY
RESONANCE|Exercise Advanced Level Problems|9 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEMS-dpp 70
- A uniform rod AB of mass m and length l at rest on a smooth horizontal...
Text Solution
|
- As shown in the figure, a disc of mass m is rolling without slipping w...
Text Solution
|
- A uniform circular disc placed on a horizontal rough surface has initi...
Text Solution
|
- The equation of motion of a particle of mass 1g is (d^(2)x)/(dt^(2)) +...
Text Solution
|
- A man of mass 60kg is standing on a platform executing SHM in the vert...
Text Solution
|
- A particle moves with a simple harmonic motion in a straight line, in ...
Text Solution
|
- A particle performing simple harmonic motion undergoes unitial displac...
Text Solution
|