Home
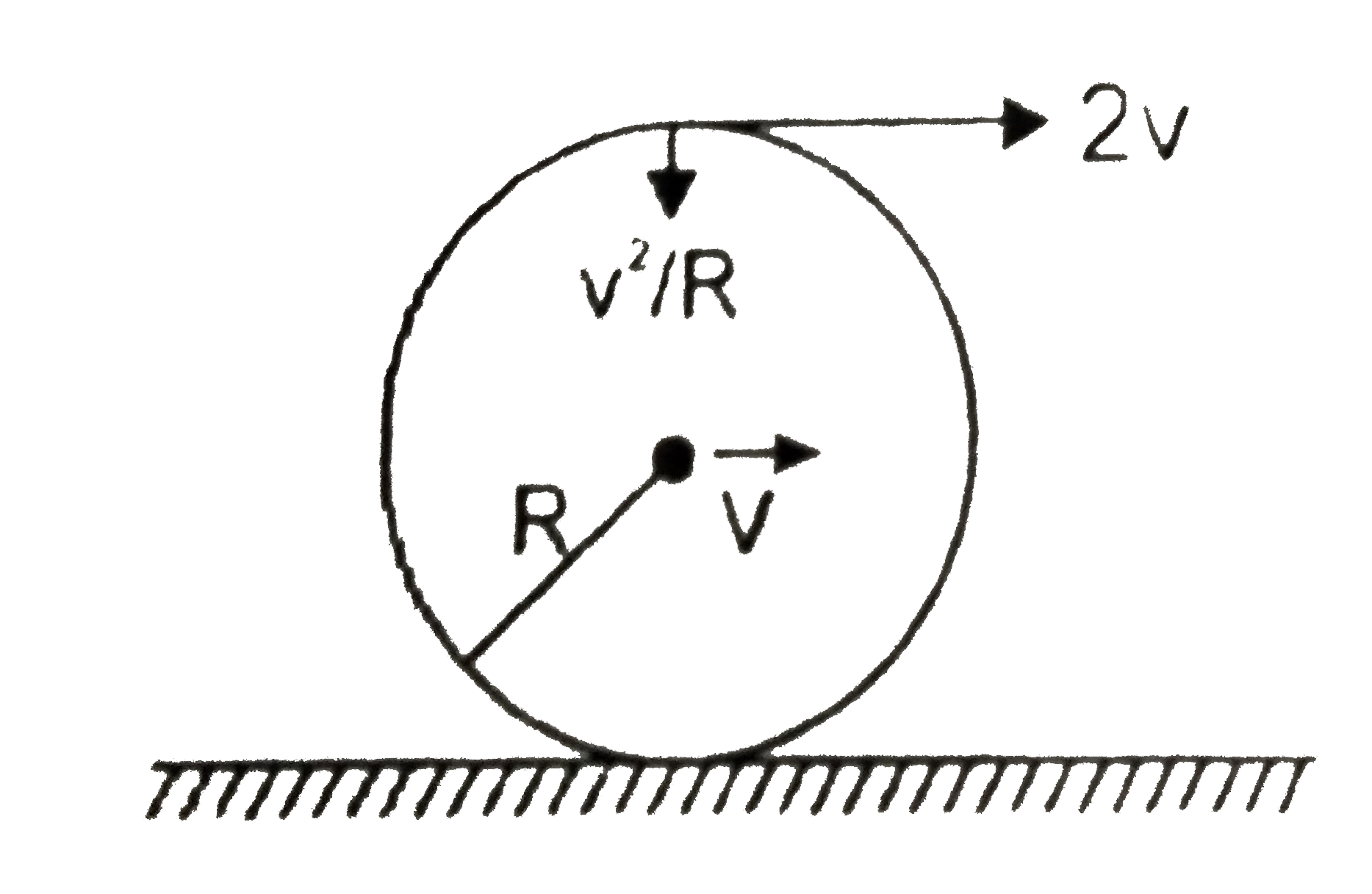
Class 11
PHYSICS
A ring of radius R rolls without slippin...

A ring of radius `R` rolls without slipping on a rough horizontal surface with a constant velocity. The radius of curvature of the path followed by any particle of the ring at the highest point of its path will be :
.

A

`3R`

B

`2R`

C

`4R`

D

none of these

Text Solution

Verified by Experts

The correct Answer is:
C
Radius of Curvature `=(("velocity")^(2))/("No rmalAccel eration")=((2v)^(2))/(v^(2)//R)=4R`
Promotional Banner

Topper's Solved these Questions

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 72|4 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp73|4 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 70|7 Videos

  • CURRENT ELECTRICITY

    RESONANCE|Exercise Exercise|54 Videos

  • ELASTICITY AND VISCOCITY

    RESONANCE|Exercise Advanced Level Problems|9 Videos

Similar Questions

Explore conceptually related problems

A wheel of radius R is rolling without sliding uniformly on a horizontal surface. Find the radius of curvature of the path of a point on its circumference when it is at highest point in its path.

The radius of curvature of the path of a charged particle moving in a static uniform magnetic field is

The radius of curvature of the path of a charged particle moving in a static uniform magnetic field is

A circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v_0 . We consider a point A on the surface of the disc. Then, the acceleration of point A is

A ring and a disc of same mass roll without slipping along a horizontal surface with same velocity. If the K.E. of ring is 8J , then that of disc is

A solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that v_(c.m.)=v_(0) .

A wheel rolls without slipping on a horizontal surface such that its velocity of center of mass is v . The velocity of a particle at the highest point of the rim is

A uniform thin ring of mass 0.4kg rolls without slipping on a horizontal surface with a linear velocity of 10 cm/s. The kinetic energy of the ring is