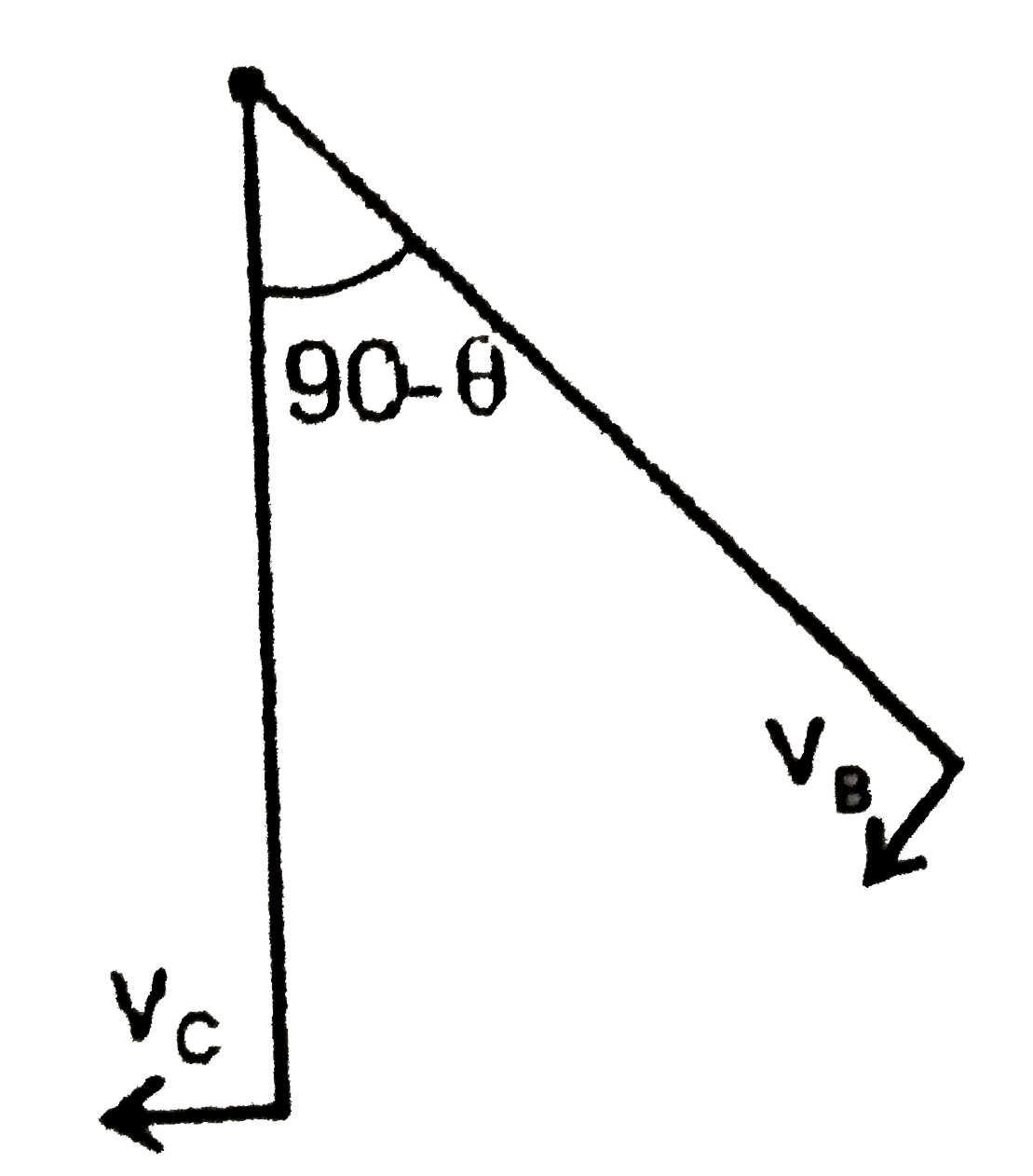
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- One end of a light string of length L is connected to a ball and the o...
Text Solution
|
- A ball of mass 1kg is attached to an inextensible string. The ball is ...
Text Solution
|
- A ball of mass 1 kg is attached to an inextensible string. The ball is...
Text Solution
|
- Three identical balls are connected by light inextensible strings with...
Text Solution
|
- One end of a light string of length L is connected to a ball and the o...
Text Solution
|
- One end of a light of length L is connected to a ball and other end is...
Text Solution
|
- One end of a light string of length L is connected to a ball and the o...
Text Solution
|
- One end of a light string of length L is connected to a ball and the o...
Text Solution
|
- One end of a light string of length L is connected to a ball and the o...
Text Solution
|