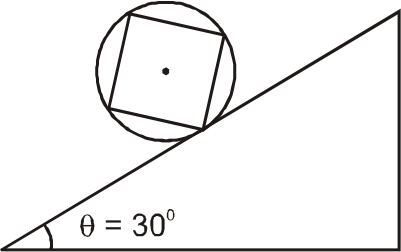
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Four identical uniform rods of mass M=6kg each are welded at their end...
Text Solution
|
- Four identical uniform rods of mass M=6kg each are welded at their end...
Text Solution
|
- Four identical uniform rods of mass M=6kg each are welded at their end...
Text Solution
|
- Four identical uniform rods of mass M=6kg each are welded at their end...
Text Solution
|
- A uniform rod of mass m is supported on two rollers each of mass m//2 ...
Text Solution
|
- A drum of radius R and mass M, rolls down without slipping along an in...
Text Solution
|
- A drum of radius R and mass M, rolls down without slipping along an in...
Text Solution
|
- For identical rods, each of mass m are welded at their ends to form a ...
Text Solution
|
- A drum of radius R and mass M, rolls down without slipping along an in...
Text Solution
|