Similar Questions
Explore conceptually related problems
Recommended Questions
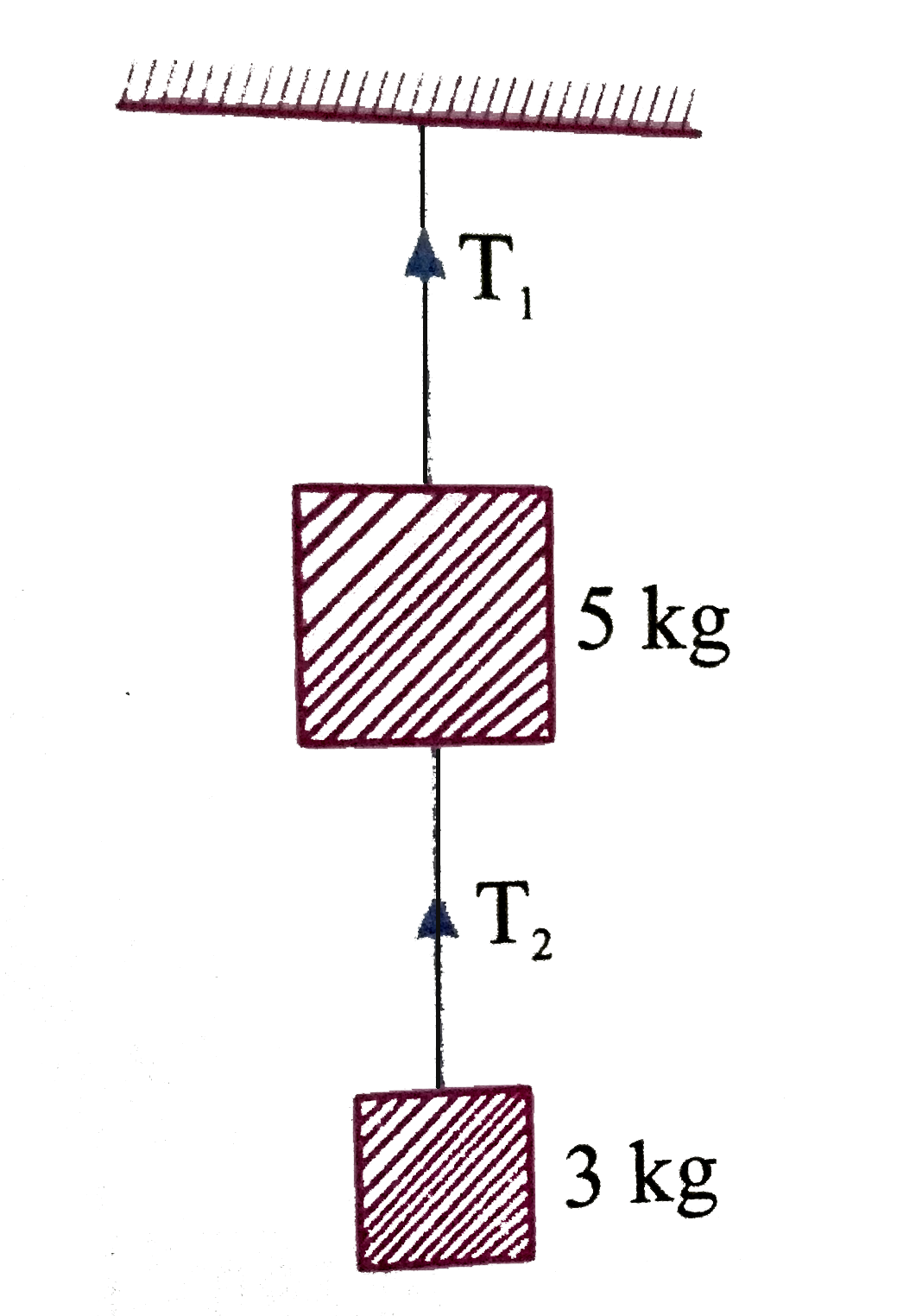
- Two masses of 5kg and 3kg are suspended with help of massless inextens...
Text Solution
|
- In the system shown in figure pully is smooth. Strings is massless and...
Text Solution
|
- Two masses of 5 kg and 3 kg are suppended with help of massless inexte...
Text Solution
|
- Two masses of 5kg and 3kg are suspended with help of massless inextens...
Text Solution
|
- Two blocks A and B of masses 2m and respectively, are connected by a ...
Text Solution
|
- Two blocks A and B of masses 2m and respectively, are connected by a ...
Text Solution
|
- A system is at rest as shown in figure. The tension in the string in T...
Text Solution
|
- Two masses of 5 kg and 3 kg are suspended with help of mass less inext...
Text Solution
|
- The masses M(1), M(2) and M(3) are 5, 2 and 3 kg respectively. These h...
Text Solution
|