Home
Class 11
PHYSICS
A ring of radius R lies in vertical plan...

A ring of radius `R` lies in vertical plane. A bead of mass `'m'` can move along the ring without friction. Initially the bead is at rest the bottom most point on ring. The minimum horizontal speed `v` with which the ring must be pulled such that the bead completes the vertical circle.

A

`sqrt(3gR)`

B

`sqrt(4 gR)`

C

`sqrt(5 gR)`

D

`sqrt(5.5 gR)`

Text Solution

Verified by Experts

The correct Answer is:
B
In the frame of ring (inertial w.r.t earth), the initial velocity of the bead is v at the lowest position.

The condition for bead to complete the vertical circle is, its speed at top position
`v_("top")ge 0`
From conservation of energy
`1/2 m v_("top")^(2)+mg(2R)=1/2 mv^(2)`
or `v=sqrt(4gR)`
Promotional Banner

Topper's Solved these Questions

  • CENTRE OF MASS

    RESONANCE|Exercise Exercise|44 Videos

  • COMMUNICATION SYSTEM

    RESONANCE|Exercise Exercise|30 Videos

Similar Questions

Explore conceptually related problems

A bead of mass m is fitted on a rod and can move on it without friction. Initially the bead is at the middle of the rod moves transitionally in the vertical plane with an accleration a_(0) in direction forming angle alpha with the rod as shown. The acceleration of bead with respect to rod is: z

A ring of radius 4a is rigidly fixed in vertical position on a table. A small disc of mass m and radius a is released as shown in the fig. When the disc rolls down, without slipping, to the lowest point of the ring, then its speed will be

A massless ring hangs from a thread and two beads of mass m slide it without friction. The beads are released simultaneously from the top of the ring and slide down along possible sides. Find the angle from vertical at which the ring will start to rise.

A ring of mass M hangs from a thread and two beads of mass m slides on it without friction. The beads are released simultaneously from the top of the ring and slides down in opposite sides. Show that the ring will start to rise, if mgt(3M)/(2) . ltbr.

The figure shows a thin ring of mass M=1kg and radius R=0.4m spinning about a vertical diameter (take I=(1)/(2)MR^(2)) A small beam of mass m=0.2kg can slide without friction along the ring When the bead is at the top of the ring the angular velocity is 5rad//s What is the angular velocity when the bead slips halfwat to theta=45^(@) ?

A ring of radius R is rolling purely on the outer surface of a pipe of radius 4R At some instant the center of the ring has constant speed =v then the acceleration of the point on the ring which is in contact with the surface of the pipe is

A bead of mass m can slide without friction along a vertical ring of radius R. One end of a spring of force constant k=(3mg)/(R ) is connected to the bead and the other end is fixed at the centre of the ring. Initially, the bead is at the point A and due to a small push it starts sliding down the ring. If the bead momentarily loses contact with the ring at the instant when the spring makes an angle 60^(@) with the vertical, then the natural length of the spring is

An isolated smooth ring of mass M = 2m with two small beads each of mass m is as shown in the figure. Initially both the beads are at diametrically opposite points and have velocity v_(0) (for each) in same direction. The speed of the beads just before they collide for the first time is (complete system is placed on a smooth horizontal surface and assume each point of ring is touching the surface)

A bead of mass m moves on a rod without friction. Initially the bead is at the middle of the rod and the rod moves translationally in a vertical plane with an acceleration a_(0) in a direction forming angle theta with the horizontal as shown in the given figure. The acceleration of bead with respect to rod is

A ring of radius r is rotating about a vertical axis along its diameter with constant angular velocity omega.A read of mass m remains at rest w.r.t. ring at the position shown in figure. Then w^(2) is:

RESONANCE-CIRCULAR MOTION-Exercise
  1. In the figure shown a lift goes downwards with a constant retardation....

    Text Solution

    |

  2. In the motorcycle stunt called " the well of death" the track is verti...

    Text Solution

    |

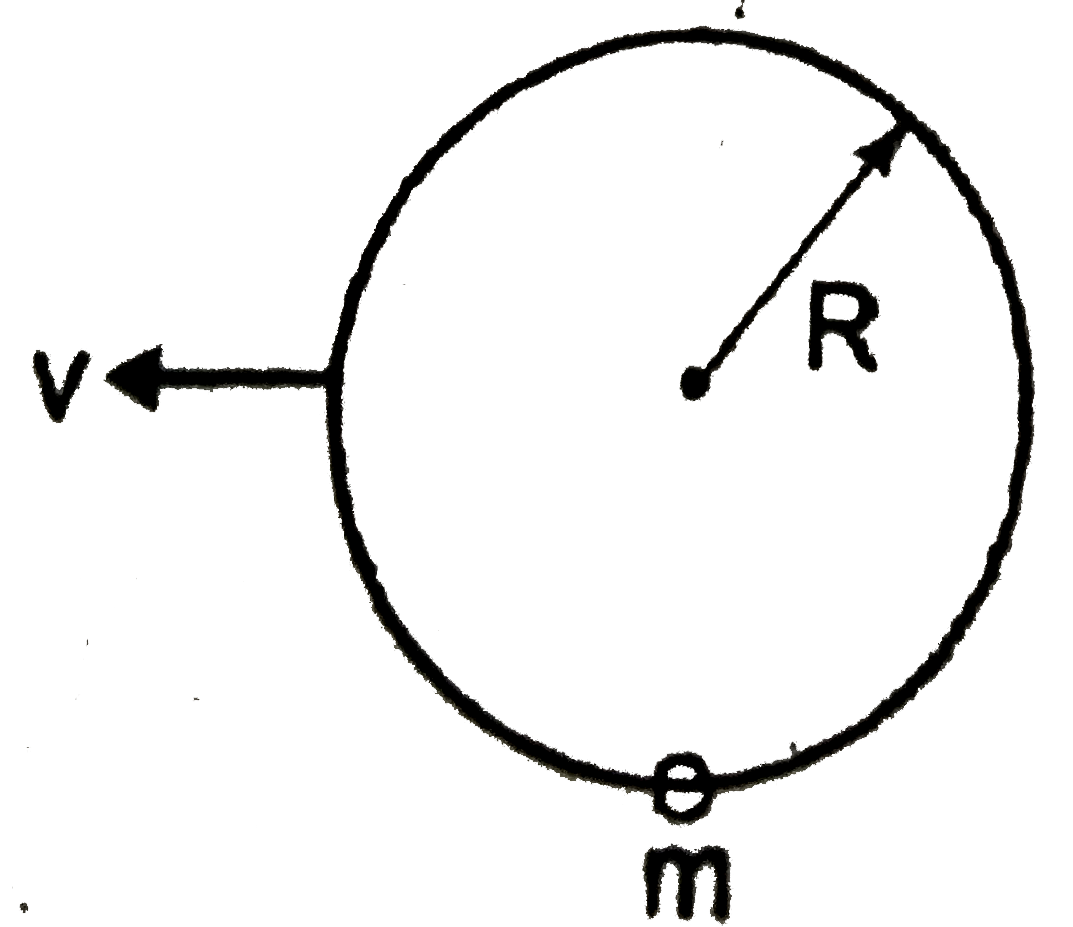
  3. A ring of radius R lies in vertical plane. A bead of mass 'm' can move...

    Text Solution

    |

  4. A circular curve of a highway is designed for traffic moving at 72 km/...

    Text Solution

    |

  5. A section of fixed smooth circular track of radius R in vertical plane...

    Text Solution

    |

  6. A particle of mass m starts to slide down from the top of the fixed sm...

    Text Solution

    |

  7. A spot light S rotates in a horizontal plane with a constant angular v...

    Text Solution

    |

  8. A stone is projected with speed u and angle of projection is theta. Fi...

    Text Solution

    |

  9. A particle moving along a circular path due to a centripetal force hav...

    Text Solution

    |

  10. A particle is projected horizontally from the top of a tower with a ve...

    Text Solution

    |

  11. A car moving on a horizontal road may be thrown out of the road in tak...

    Text Solution

    |

  12. A stone tied to a string is rotated with a uniform speed in a vertical...

    Text Solution

    |

  13. A simple pendulum is oscillating without damiping, When the displaceme...

    Text Solution

    |

  14. A stone tied to a string of length L is whirled in a vertical circle w...

    Text Solution

    |

  15. A particle is acted upon by a force of constant magnitude which is alw...

    Text Solution

    |

  16. A bird is flying in the air. To take a turn in the horizontal plane of...

    Text Solution

    |

  17. A particle moves along a circle if radius (20 //pi) m with constant ta...

    Text Solution

    |

  18. For a body in circular motion with a constant angular velocity, the ma...

    Text Solution

    |

  19. A ball suspended by a thread swing in a vertical plane that its accel...

    Text Solution

    |

  20. The position vector of a particle in a circular motion about the origi...

    Text Solution

    |