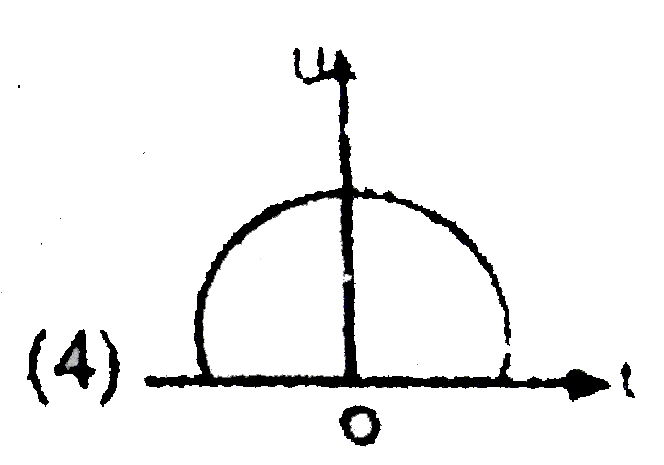A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
RESONANCE-SIMPLE HARMONIC MOTION-Exercise
- The amplitude of a particle performing SHM is 'a'. The displacement at...
Text Solution
|
- In S.H.M., the graph between kinetic energy K and time 't' is
Text Solution
|
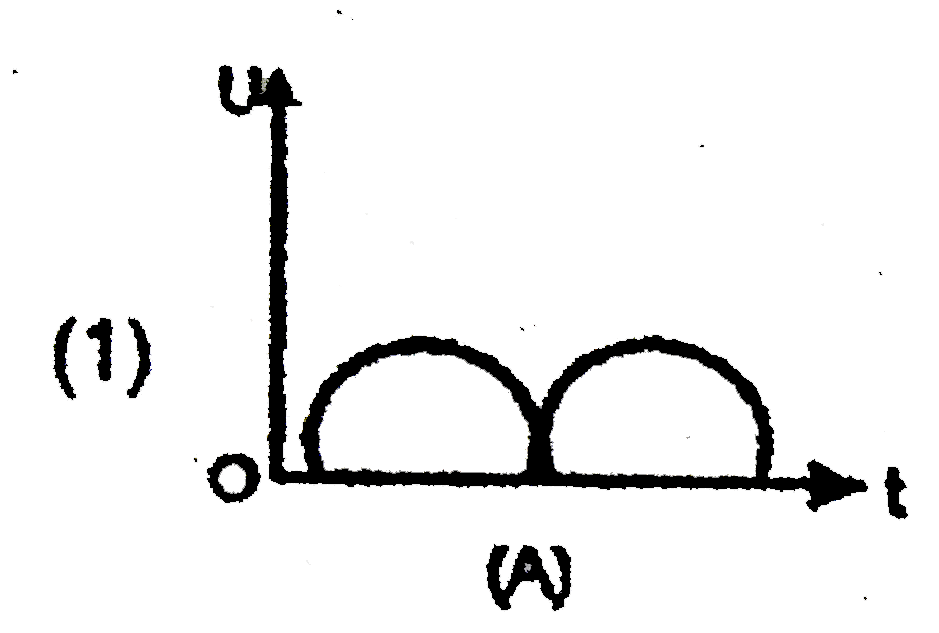
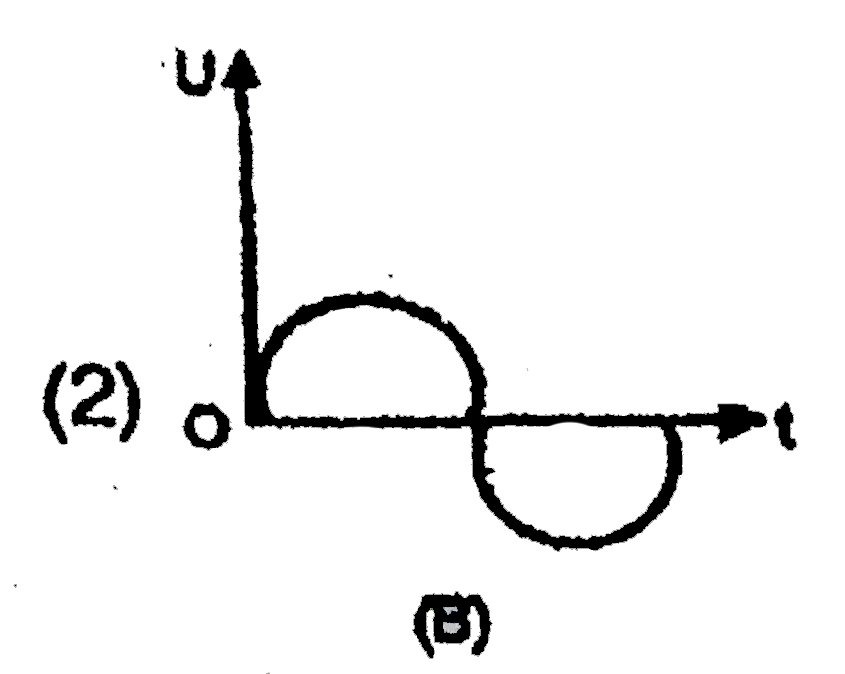
- In S.H.M., potential energy (U) V/s, time (t) . Graph is
Text Solution
|
- The variation of the acceleration (f) of the particle executing S.H.M....
Text Solution
|
- The graph in the figure shows how the displacement of a particle descr...
Text Solution
|
- For a simple harmonic vibrator frequency n, the frequency of kinetic e...
Text Solution
|
- A particle is executing SHM with an amplitude 4 cm. the displacment at...
Text Solution
|
- For a particle executing S.H.M. which of the following statements hold...
Text Solution
|
- The equation of SHM of a particle is (d^2y)/(dt^2)+ky=0, where k is a ...
Text Solution
|
- The total energy of the body excuting S.H.M. is E . Then the kinetic e...
Text Solution
|
- A linear harmonic oscillator of force constant 2 xx 10^6 N//m and ampl...
Text Solution
|
- A particle excuting S.H.M. of amplitude 4 cm and T = 4 sec .The time t...
Text Solution
|
- The potential energy of a particle execuring S.H.M. is 2.5 J, when its...
Text Solution
|
- A body of mass m is suspended from three springs as shown in figure. I...
Text Solution
|
- One mass m is suspended from a spring. Time period of oscilation is T....
Text Solution
|
- A spring has a certain mass suspended from it and its period for verti...
Text Solution
|
- Two objects A and B of equal mass are suspended from two springs const...
Text Solution
|
- If the period of oscillation of mass M suspended from a spring is one ...
Text Solution
|
- A simple pendulum suspended from the ceilling of a stationary trolley ...
Text Solution
|
- If length of simple pendulum is increased by 6% then percentage change...
Text Solution
|