Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
RESONANCE-NUCLEAR PHYSICS-Advanced level solutions
- A radioactive element decays by beta-emission. A detector records n be...
Text Solution
|
- A 100ml solution having activity 50 dps is kept in a beaker It is now ...
Text Solution
|
- what kinetic energy must an alpha-particle possess to split a deuteron...
Text Solution
|
- Suppose a nucleus initally at rest undergoes alpha decay according to...
Text Solution
|
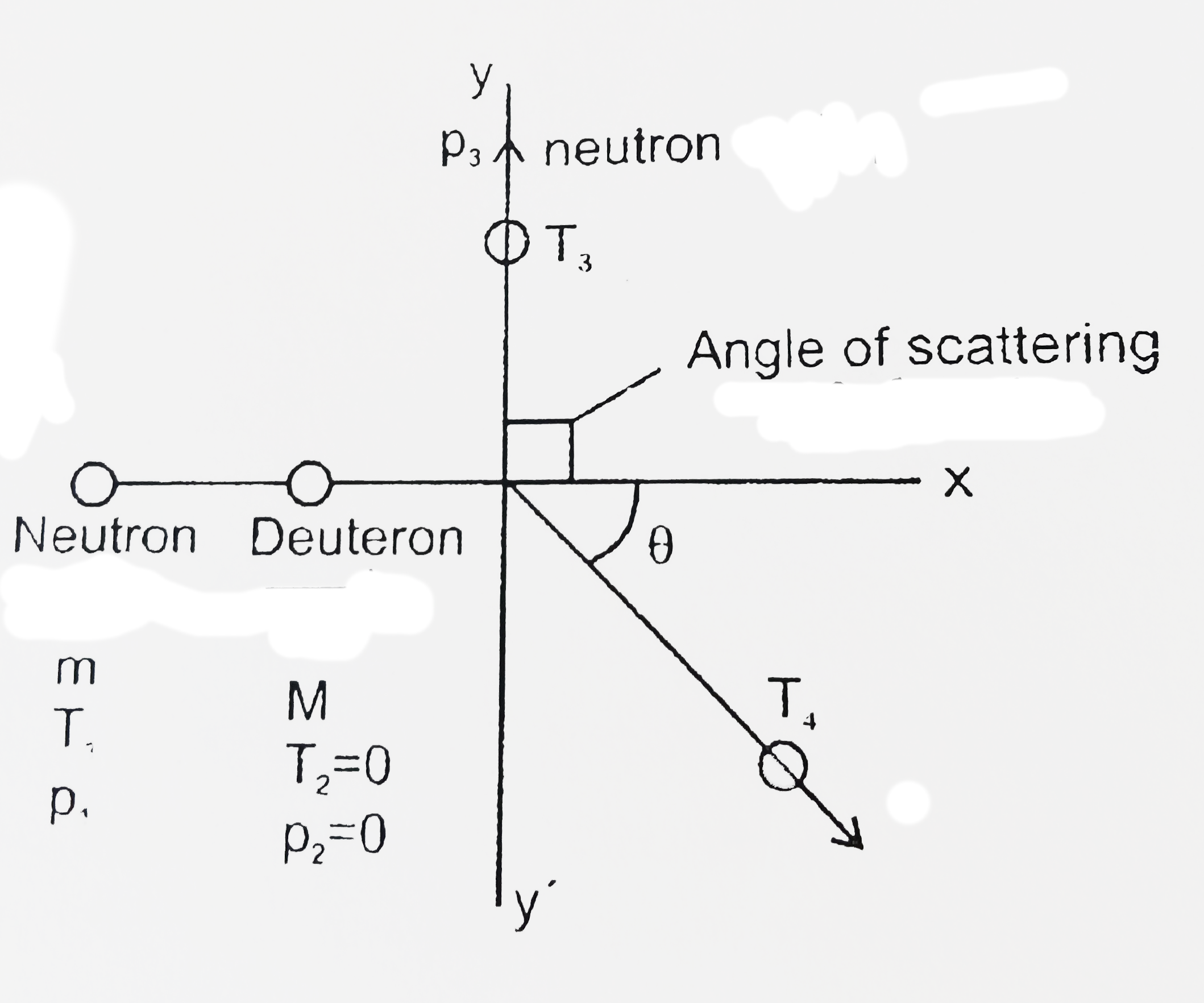
- A neutron collides elastically with an initially stationary deuteron. ...
Text Solution
|
- Find the binding energy of a nucleus consisting of equal numbers of pr...
Text Solution
|
- A radio nuclide with half life T = 69.31 second emits beta-particles ...
Text Solution
|
- (a) Find the energy needed to remove a neutron from the nucleus of the...
Text Solution
|
- A nucleus X, initially at rest , undergoes alpha dacay according to th...
Text Solution
|
- 100 millicuries of radon which emits 5.5 MeV alpha- particles are cont...
Text Solution
|
- Radium being a member of the uranium series occurs in uranium ores. If...
Text Solution
|
- .^(90)Sr decays to .^(90)Y by beta decay with a half-life of 28 years....
Text Solution
|
- The element Curium (96)^(248Cm has a mean life of 10^(13) second. Its ...
Text Solution
|
- Nucleus .(3)A^(7) has binding energy per nucleon of 10 MeV. It absorbs...
Text Solution
|
- The nucleus of .(90)^(230)Th is unstable against alpha-decay with a ha...
Text Solution
|
- When .^(30)Si bombarded with a deutron. .^(31)Si is formed in its grou...
Text Solution
|