Similar Questions
Explore conceptually related problems
Recommended Questions
- If a stone is to hit at a point which is at a distance d away and at a...
Text Solution
|
- A heavy stone is thrown from a cliff of height h with a speed v. The s...
Text Solution
|
- From an elevated point A, a stone is projected vertically upwards. Whe...
Text Solution
|
- A stone thrown upwards with speed u attains maximum height h. Ahother ...
Text Solution
|
- If a stone is to hit at a point which is at a distance d away and at a...
Text Solution
|
- If a ston s to at a point which is at a distance d away and at a heigh...
Text Solution
|
- If a stone is to hit at a point which is at a distance d away and at a...
Text Solution
|
- A heavy stone is thrown from a cliff of height h with a speed .v. The...
Text Solution
|
- If a stone is to hit at a point which is at a horizontal distance 100 ...
Text Solution
|
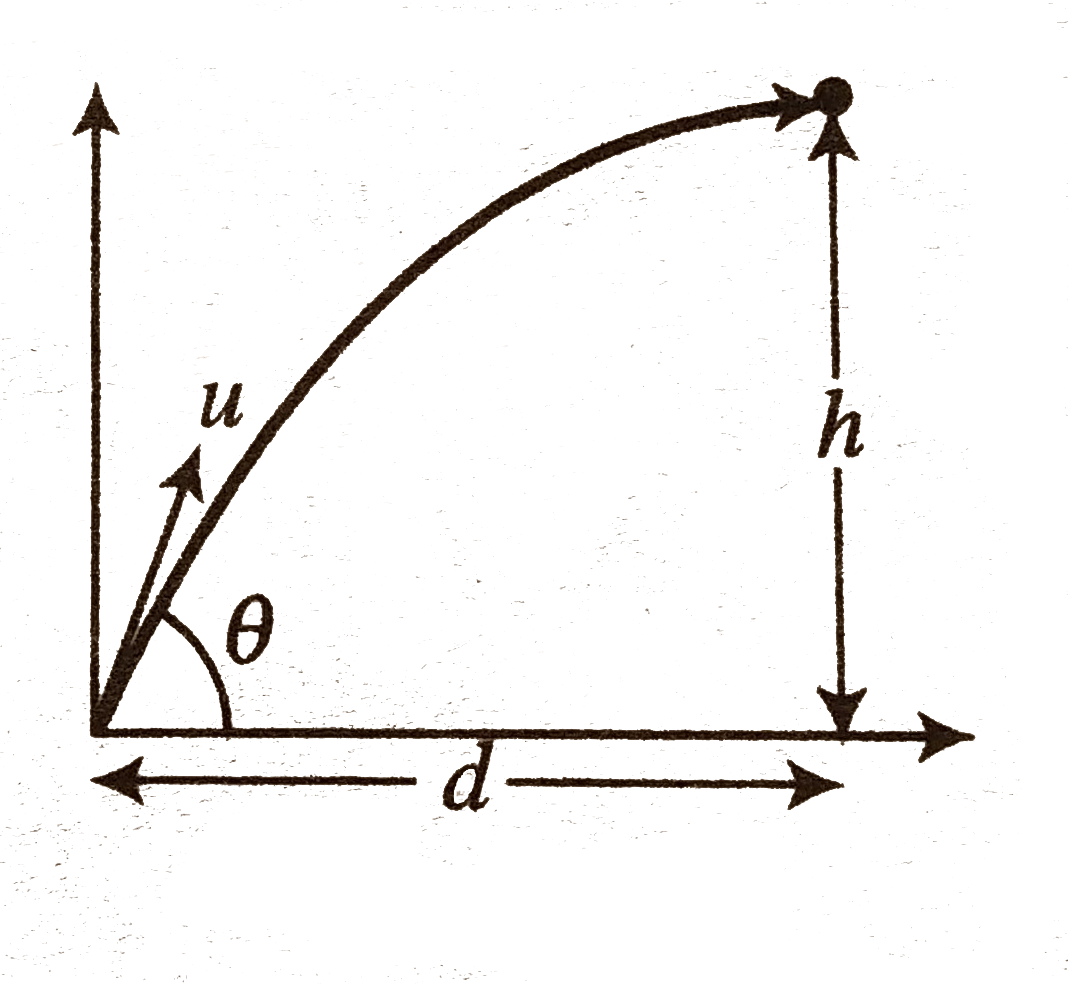 .
.