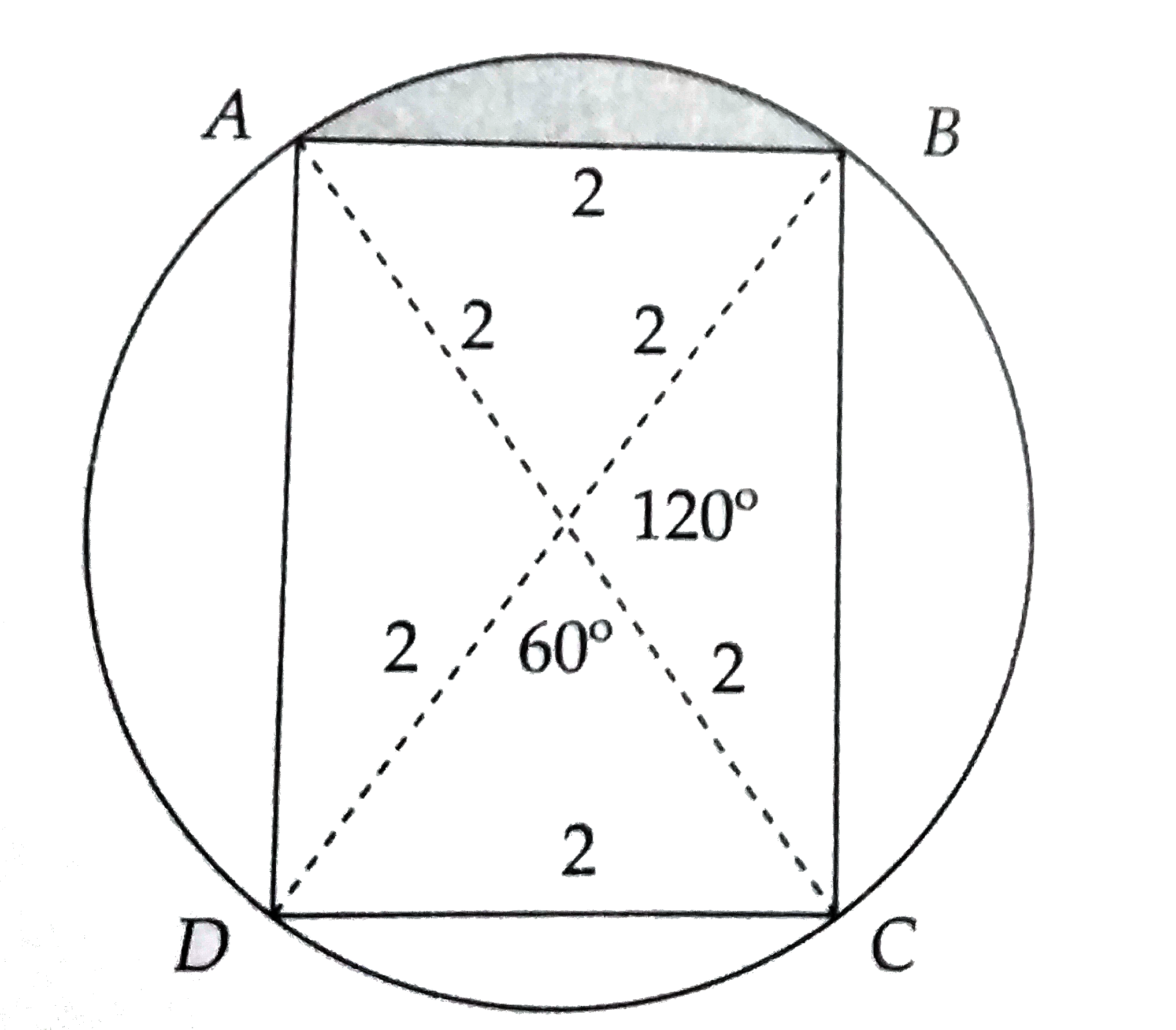
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
KAPLAN-PLANE GEOMETRY -PLANE GEOMETRY FOLLOW - UP TEST
- Rectangle ABCD is inscribed in a circle. If the radius of the circle i...
Text Solution
|
- The ratio of bar(DB) to bar(EF) is 4 to 9. If bar(DF)=2, what is the ...
Text Solution
|
- In Delta YVW in Figure, bar(VX) is the altitude to side bar(YW), and b...
Text Solution
|
- bar(EG)|| bar(DH), and the length of segments bar(DE) and bar(EF) are ...
Text Solution
|
- If bar(XY) = 3, what is the area of Delta XYZ ?
Text Solution
|
- The area of parallelogram JKLM is 28 bar(JK)=7. If bar(KN) is perpendi...
Text Solution
|
- Points P, Q, and R lie on the circumference of the circle centered at ...
Text Solution
|