A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
KAPLAN- TRIGONOMETRY-Multiple Choice Question
- Davis drew a unit circle and labeled the cosine and sine of 45^(@) as ...
Text Solution
|
- The right triangle above, cosx=0.8. What is the value of cosy?
Text Solution
|
- Right triangle ABC has side lengths 7, 24, and 25. If angleB is the s...
Text Solution
|
- If the longer leg of a right triangle has length 32 centimeters, and t...
Text Solution
|
- In the triangle above, tanx=(sqrt(7))/(3). What is cosx?
Text Solution
|
- If (cost)/(cost)=(1)/(3), then what is tant?
Text Solution
|
- Triangle BUG shown is an isosceles right triangle. If the length of si...
Text Solution
|
- In a right triangle, one angle measure x^(@), where sinx^(@)=(5)/(15)....
Text Solution
|
- The angles of a triangle are in the ratio 1:2:3. What is the sine of t...
Text Solution
|
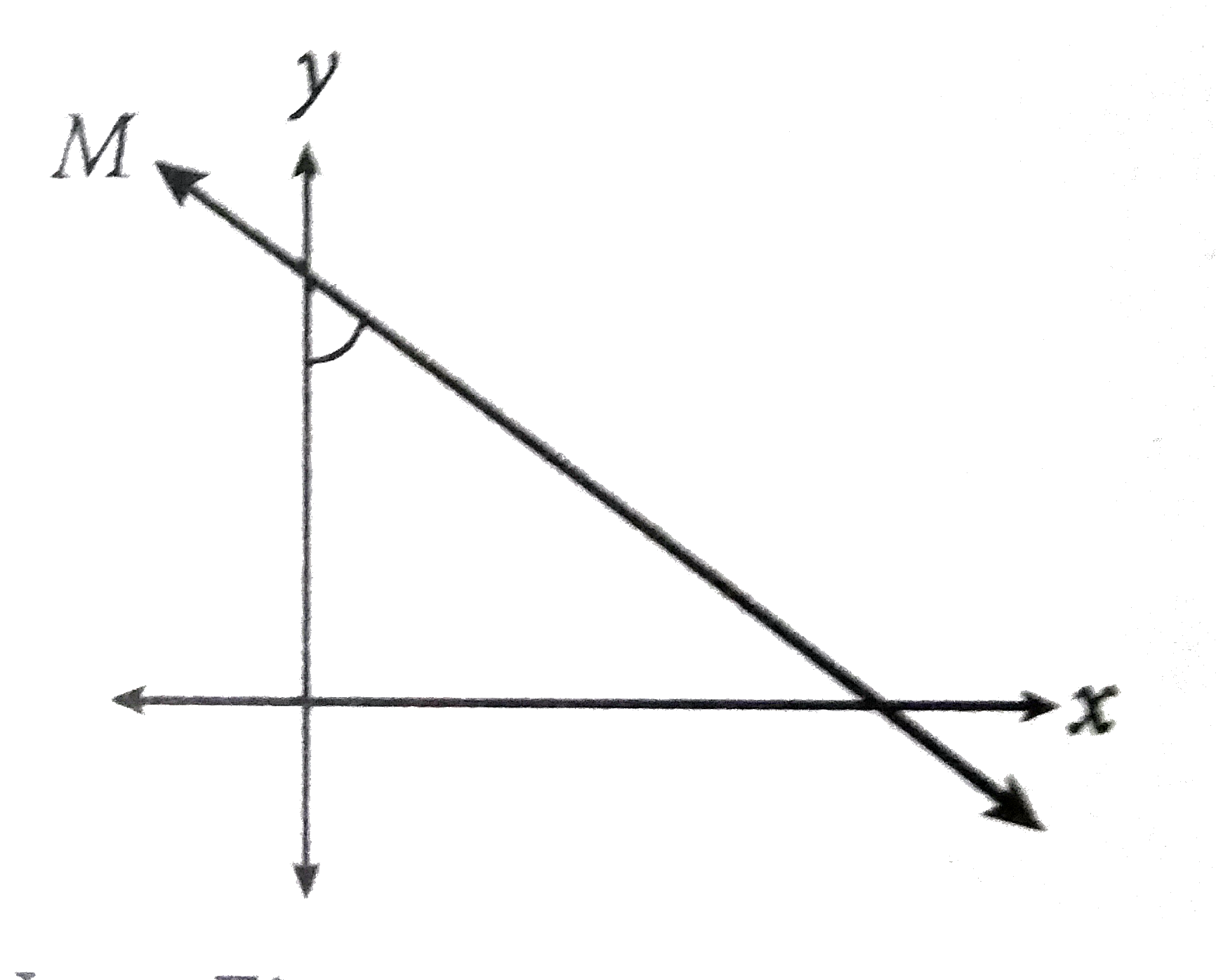
- The equation of line M shown above is y=-(3)/(4)x+5. Given that angle ...
Text Solution
|
- If the area of the triangle shown above is 12 squares inches, what is ...
Text Solution
|
- In triangle XYZ (not shown), the measure of angleY is 90^(@), YZ=12, a...
Text Solution
|