Similar Questions
Explore conceptually related problems
Recommended Questions
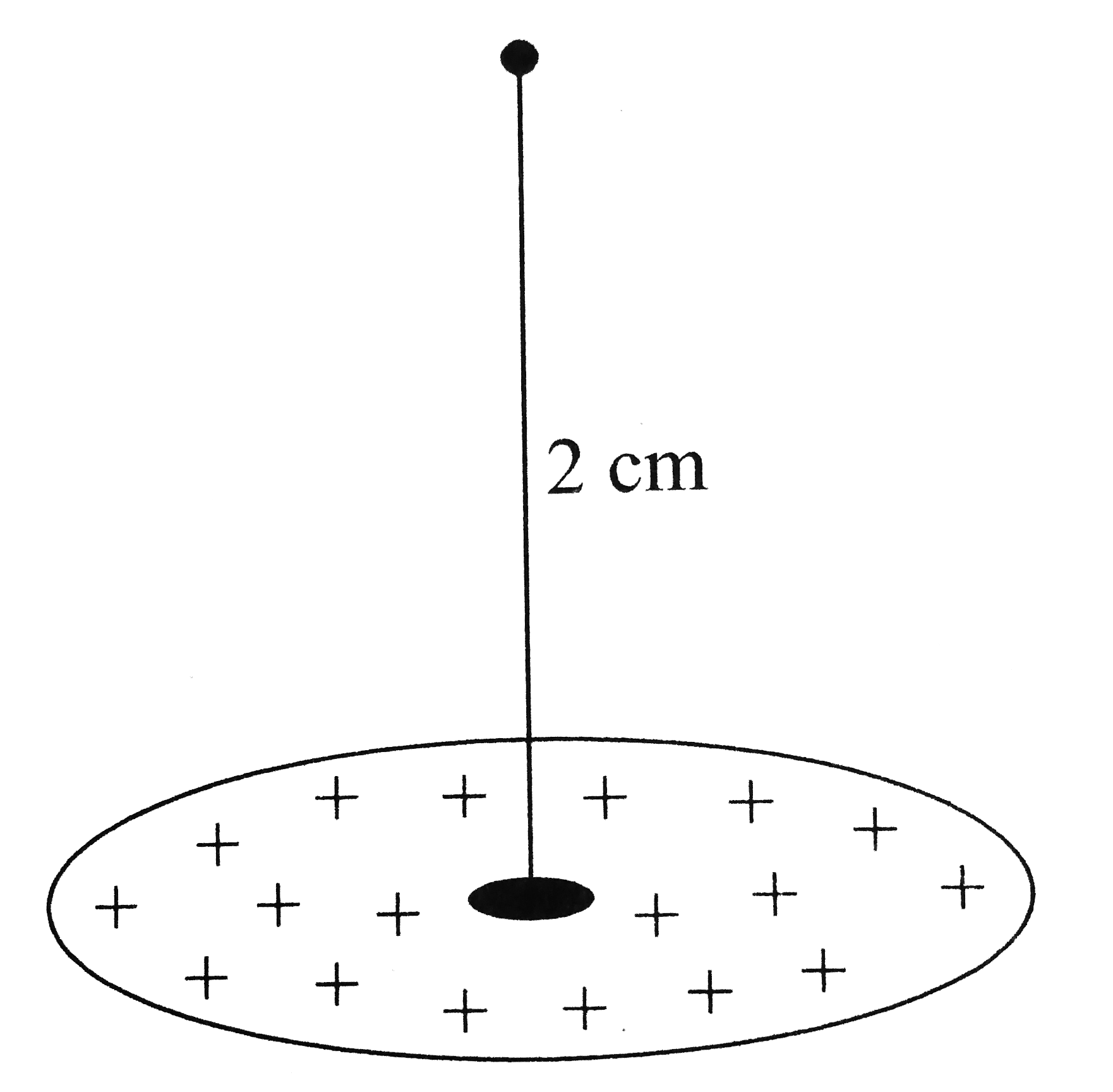
- A uniformly charged non conducting disc with surface charge density 10...
Text Solution
|
- A uniformly charged non conducting disc with surface charge density 10...
Text Solution
|
- Calculate electric field at a point on axis, which at a distance x fro...
Text Solution
|
- A Uniformly charged solid non-conducting sphere of uniform volume char...
Text Solution
|
- Find out electric field intensity due to uniformly charged solid non-c...
Text Solution
|
- The electric field intensity in free space at a distance 'r' outside a...
Text Solution
|
- एकसमान आवेशित छड़ जिसकी लम्बाई 2l तथा कुल आवेश q है, के कारण उसके लम्ब...
Text Solution
|
- The electric field intensity in free space at a distance 'r' outside a...
Text Solution
|
- A non conducting solid sphere of radius R is uniformly charged. The ma...
Text Solution
|