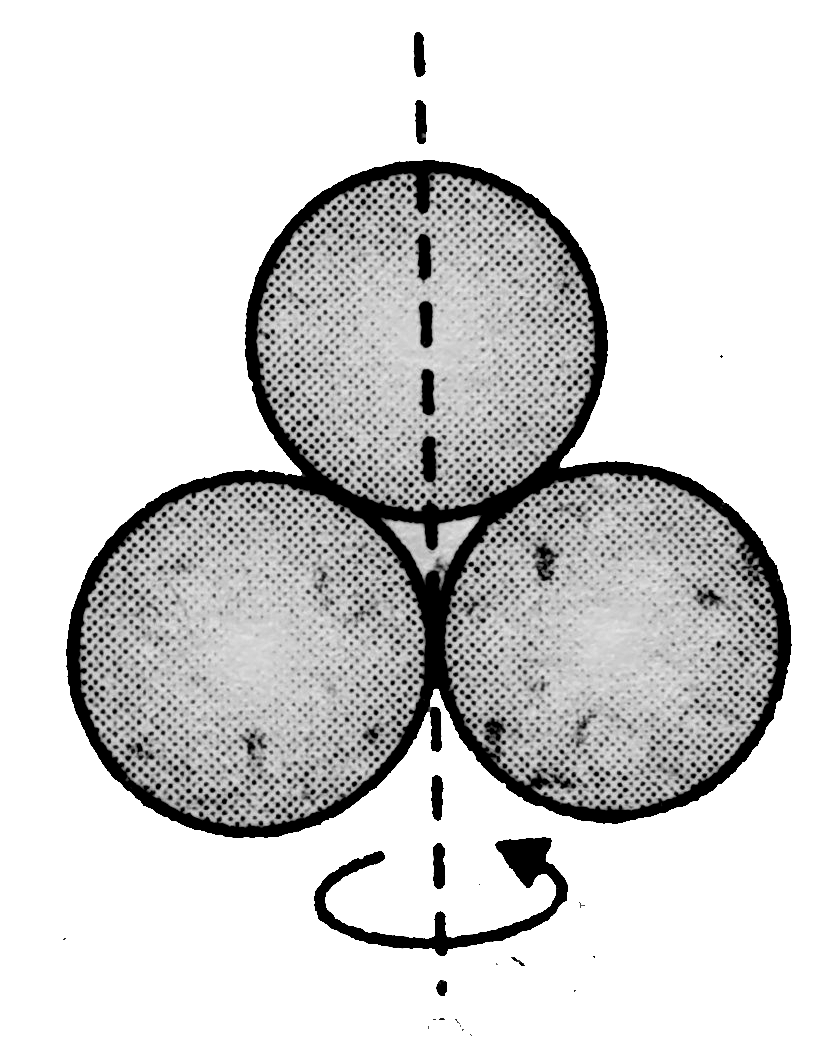
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Three rings, each of mass m and radius r, are so placed that they touc...
Text Solution
|
- Three rings, each of mass m and radius r, are so placed that they touc...
Text Solution
|
- Three rings each of mass m and radius r are so placed that they touch ...
Text Solution
|
- A wheel comprises a ring of radius R and mass M and three spokes of ma...
Text Solution
|
- Three rings, each of mass P and radius Q are arranged as shown in the ...
Text Solution
|
- Three rings each of mass M and radius R are placed in contact with eac...
Text Solution
|
- Thee spheres each of mass M and radius R are placed in contact with ea...
Text Solution
|
- Four rings each of mass M and radius R are arranged as shown in the fi...
Text Solution
|
- Two identical concentric rings each of mass m and radius R are placed ...
Text Solution
|