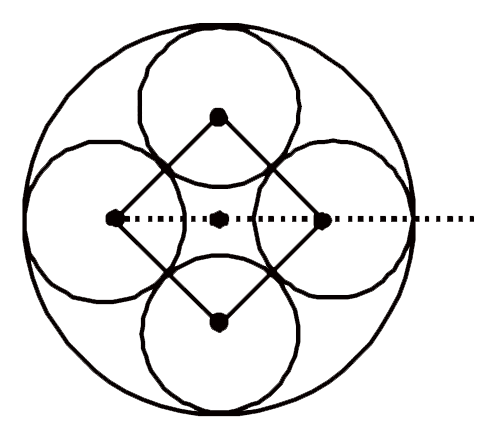
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Four identical spheres having mass M and radius R are fixed tightly wi...
Text Solution
|
- A ring of mass m=1kg can slide over a smooth vertical rod. A light str...
Text Solution
|
- An impulse J is applied on a ring of mass m along a line passing throu...
Text Solution
|
- Four identical spheres having mass M and radius R are fixed tightly wi...
Text Solution
|
- Four identical spheres having mass M and radius R are fixed tightly wi...
Text Solution
|
- Four identical spheres having mass M and radius R are fixed tightly wi...
Text Solution
|
- A smooth ring of mass m can slide on a fixed horizontal rod. A string ...
Text Solution
|
- A ring of mass m and radius R is placed on a rough inclined plane so t...
Text Solution
|
- A ring of mass M and radius R is at rest at the top of an incline as s...
Text Solution
|