Home
Class 12
PHYSICS
A region has a uniform magnetic field B ...

A region has a uniform magnetic field B along positive x direction and a uniform electric field E in negative x direction. A positively charged particle is projected from origin with a velocity `underset(V)to=V_(0)hati+V_(0)hatj` . After some time the velocity of the particle was observed to be`V_(0)hatJ` while its x co-ordinate was positive. Write all possible values of `(E)/(B)`

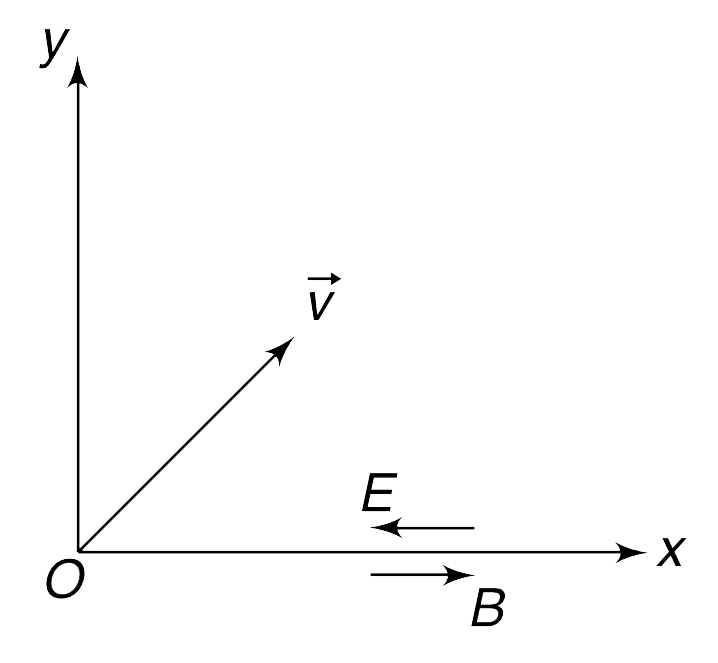
Text Solution

Verified by Experts

The correct Answer is:
`E/B=(v_(0))/(2pin) "where" n=1,2,3….`
Promotional Banner

Topper's Solved these Questions

  • MOTION OF CHARGE IN MAGNETIC FIELD

    ARIHANT|Exercise Level-2|13 Videos

  • MOTION OF CHARGE IN MAGNETIC FIELD

    ARIHANT|Exercise Level-3|4 Videos

  • MAGNETIC EFFECT OF CURRENT

    ARIHANT|Exercise Magnetic effect of Current|45 Videos

  • NUCLEAR PHYSICS

    ARIHANT|Exercise All Questions|54 Videos

Similar Questions

Explore conceptually related problems

A uniform electric field, underset(E)to=E_(0)hati and a uniform magnetic field, underset(B)to=B_(0)hati exist in region y gt 0. A particle hav- ing positive charge q and mass m is projected from the origin with a velocity underset(V)to=V_(0)hati+V_(0)hatJ. The velocity of the particle when it leaves the region of fields was found to be -underset(V)to. (i) Find the ratio (E_(0))/(B_(0)) in terms of v0. (ii) Find the co-ordinates of the point where the particle leaves the fields. (iii) Find the minimum speed of the particle during the course of the motion.

A proton is fired from origin with velocity vecv=v_0hatj+v_0hatk in a uniform magnetic field vecB=B_0hatj .

A particle of specific charge alpha is projected from origin with velocity v=v_0hati-v_0hatk in a uniform magnetic field B=-B_0hatk . Find time dependence of velocity and position of the particle.

A charged particle (q.m) released from origin with velocity v=v_(0)hati in a uniform magnetic field B=(B_(0))/(2)hati+(sqrt3B_(0))/(2)hatJ . Pitch of the helical path described by the particle is

A charged particle (q.m) released from origin with velocity v=v_(0)hati in a uniform magnetic field B=(B_(0))/(2)hati+(sqrt3B_(0))/(2)hatJ . Maximum z-coordinate of the particle is

Electric field strength bar(E)=E_(0)hat(i) and bar(B)=B_(0)hat(i) exists in a region. A charge is projected with a velocity bar(v)=v_(0)hat(j) at origin , then

A projectile is projected from ground with initial velocity vecu=u_(0)hati+v_(0)hatj . If acceleration due to gragvity (g) is along the negative y-direction then find maximum displacement in x-direction.

In the XY- plane , the region y gt 0 has a uniform magnetic field B_1 hatk and the region y lt 0 has another uniform magnetic field B_2 hatk . A positively charged particle is projected from the origin along the positive y- axis with speed v_0= pi m s^(-1) at t=0 , as shown in the figure . Neglect gravity in this problem . Let t=T be the time when the particle crosses the X- axis from below for the first time . If B_2 = 4B_1 , the average speed to the particle , in ms^(-1) , along the x- axis in the time interval T is __________ .

Electric field and magnetic fiedl n a region of sace is given by E=E_0hatj and B=B_0hatj . A particle of specific charge alpha is released from origin with velocity v=v_0hati . Then path of particel