Home
Class 12
PHYSICS
Two particles have equal mass m and elec...

Two particles have equal mass m and electric charge of equal magnitude (q) and opposite sign. The particles are held at rest at co-ordinates (– a, 0) and (a, 0) as shown in the figure. The particles are released simultaneously. Consider only the electrostatic force between the particles and the force applied by the external magnetic field on them.

(a) Find the speed of negatively charged particle as function of its x co-ordinate.
(b) Find the y component of velocity of the negative particle as a function of its x co-ordinate.

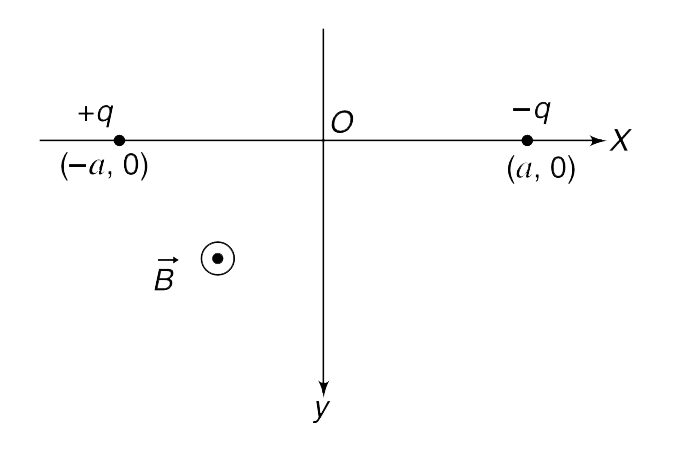
Text Solution

Verified by Experts

The correct Answer is:
`(a) V=sqrt(kq^(2)/(2m)(1/x-1/a))" "(b) V_(y)=(qB)/(m)(a-x)`
Promotional Banner

Topper's Solved these Questions

  • MOTION OF CHARGE IN MAGNETIC FIELD

    ARIHANT|Exercise Level-3|4 Videos

  • MOTION OF CHARGE IN MAGNETIC FIELD

    ARIHANT|Exercise Level-3|4 Videos

  • MAGNETIC EFFECT OF CURRENT

    ARIHANT|Exercise Magnetic effect of Current|45 Videos

  • NUCLEAR PHYSICS

    ARIHANT|Exercise All Questions|54 Videos

Similar Questions

Explore conceptually related problems

Three charged particle sare in equilibrium under their electrostatic forces only. Then

A force F acts on a particle kept on a rough surface as shown in the figure. The particle is at rest. Find the net force applied by ground on the particle.

If a charged particle at rest experiences no electromagnetic force, then The electric field must be zero

A particle having mass m and charge q is released from the origin in a region in which electric field and magnetic field are given by vecB =- B_0vecJ and vecE - E_0 vecK. Find the speed of the particle as a function of its z-coordinate.

A particle having mass m and charge q is released from the origin in a region in which electric field and magnetic field are ginen by B=+B_(0)hatj and vecE=+E_(0)hati . Find the speed of the particle as a function of its X -coordinate.

A charged particle is moved along a magnetic field line. The magnetic force on the particle is

The magnetic force on a charged particle is always perpendicular to its velocity. Can the magnetic force change the velocity of the particle?Speed of the particle?

If a charged particle at rest experiences no electromagnetic force, then electric field in that region

Force acting on a moving charged particle in a region of electric and magnetic fields is called