Home
Class 11
PHYSICS
The two conducting spherical shells are ...

The two conducting spherical shells are joined by a conducting wire and cut after some time when charge stops flowing. Find out the charge on each sphere after that.

Text Solution

Verified by Experts

After cutting the wire, the potential of both the shells is equal
Thus, potential of inner shell `V_("in")=(Kx)/(R)+(K(-2Q-x))/(2R)=(K(x-2Q))/(2R)`
and potential of outer shell `V_("out")=(Kx)/(2R)+(K(-2Q-x))/(2R)=(-KQ)/(R)`
As `V_("out")=V_("in")rArr (-KR)/(R)=(K(x-2Q))/(2R)rArr -2Q=x-2Q rArr x=0`
So charge on inner spherical shell `=0` and outer spherical shell `=-2 Q`
Promotional Banner

Topper's Solved these Questions

  • MISCELLANEOUS

    ALLEN|Exercise Part -II Example Some worked out Examples|1 Videos

  • MISCELLANEOUS

    ALLEN|Exercise Exercise-01|87 Videos

  • MISCELLANEOUS

    ALLEN|Exercise SUBJECTIVE QUESTION|9 Videos

  • KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)

    ALLEN|Exercise BEGINNER S BOX-7|8 Videos

  • PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT

    ALLEN|Exercise EXERCISE-IV|8 Videos

Similar Questions

Explore conceptually related problems

Figure shows three concentric conducting spherical shells with inner and outer shells earthed and the middle shell is given a charge q . Find the charge distribution of sphere

Column-I gives certain situations involving two thin conducting shells connected by a conducting wire via a key K. In all situation one sphere has net charge +q and other sphere has no net charge. After the key K is pressed, column-II gives some resulting effect.

Statement-1 : If two concentric conducing sphere which are connected by a conducting wire. No charge can exist on inner sphere. Statement-2: When charge on outer sphere will exist then potential of inner shell and outer shell will be same.

A solid metallic sphere of radius a is surrounded by a conducting spherical shell of radius b(bgt a ). The solid sphere is given a charge Q. A student measures the potential at the surface of the solid sphere as V and the potential at the surface of spherical shell as V_b . After taking these readings, he decides . to put charge of -4Q on the shell. He then noted the readings of the potential of solid sphere and the shell and found that the potential difference is /_\V . He then connected the outer spherical shell to the earth by a conducting wire and found that the charge on the outer surface of the shell as He then decides to remove the earthing connection from the shell and earthed the inner solid sphere. Connecting the inner sphere with the earth he observes the charge on the solid sphere as q_2 . He then wanted to check what happens if the two are connected by the conducting wire. So he removed the earthing connection and connected a conducting wire between the solid sphere and the spherical shelll. After the connections were made he found the charge on the outer shell as q_3 . Potential difference (/_\CV) measured by the student between the inner solid shere and outer shell after putting a charge -4Q is

When two charged bodies at different potentials are connected by a conducting wire, then the charge flows from one body to another body

A solid metallic sphere of radius a is surrounded by a conducting spherical shell of radius b(bgt a) . The solid sphere is given a charge Q. A student measures the potential at the surface of the solid sphere as V and the potential at the surface of spherical shell as V_b . After taking these readings, he decides . to put charge of -4Q on the shell. He then noted the readings of the potential of solid sphere and the shell and found that the potential difference is /_\V . He then connected the outer spherical shell to the earth by a conducting wire and found that the charge on the outer surface of the shell as He then decides to remove the earthing connection from the shell and earthed the inner solid sphere. Connecting the inner sphere with the earth he observes the charge on the solid sphere as q_2 . He then wanted to check what happens if the two are connected by the conducting wire. So he removed the earthing connection and connected a conducting wire between the solid sphere and the spherical shelll. After the connections were made he found the charge on the outer shell as q_3 . q_2 is

A solid metallic sphere of radius a is surrounded by a conducting spherical shell of radius b(bgt a) . The solid sphere is given a charge Q. A student measures the potential at the surface of the solid sphere as V and the potential at the surface of spherical shell as V_b . After taking these readings, he decides . to put charge of -4Q on the shell. He then noted the readings of the potential of solid sphere and the shell and found that the potential difference is /_\V . He then connected the outer spherical shell to the earth by a conducting wire and found that the charge on the outer surface of the shell as He then decides to remove the earthing connection from the shell and earthed the inner solid sphere. Connecting the inner sphere with the earth he observes the charge on the solid sphere as q_2 . He then wanted to check what happens if the two are connected by the conducting wire. So he removed the earthing connection and connected a conducting wire between the solid sphere and the spherical shelll. After the connections were made he found the charge on the outer shell as q_3 . q_3 is

A point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.

When two concentric shells are connected by a thin conducting wire, whole of the charge of inner shell transfers to the outer shell and potential difference between them becomes zero. Surface charge densities of two thin concentric spherical shells are sigma and -sigma respectively. Their radii are R and 2R . Now they are connected by a thin wire. Suppose electric field at a distance r (gt 2R) was E_(1) before connecting the two shells and E_(2) after connecting the two shells, then |E_(2)/E_(1)| is :-

When two concentric shells are connected by a thin conducting wire, whole of the charge of inner shell transfers to the outer shell and potential difference between them becomes zero. Surface charge densities of two thin concentric spherical shells are sigma and -sigma respectively. Their radii are R and 2R . Now they are connected by a thin wire. Suppose electric field at a distance r=(3R)/2 was E_(1) before connecting the two shells and E_(2) after connecting the two shells, then |E_(2)/E_(1)| is :-

ALLEN-MISCELLANEOUS-Part -II Example
  1. An unchanged conductor of inner radius R(1) and outer radius R(2) cont...

    Text Solution

    |

  2. When the switch is closed find the charge flown through switch?

    Text Solution

    |

  3. The two conducting spherical shells are joined by a conducting wire an...

    Text Solution

    |

  4. Find charge on each spherical shell after joining the inner most shell...

    Text Solution

    |

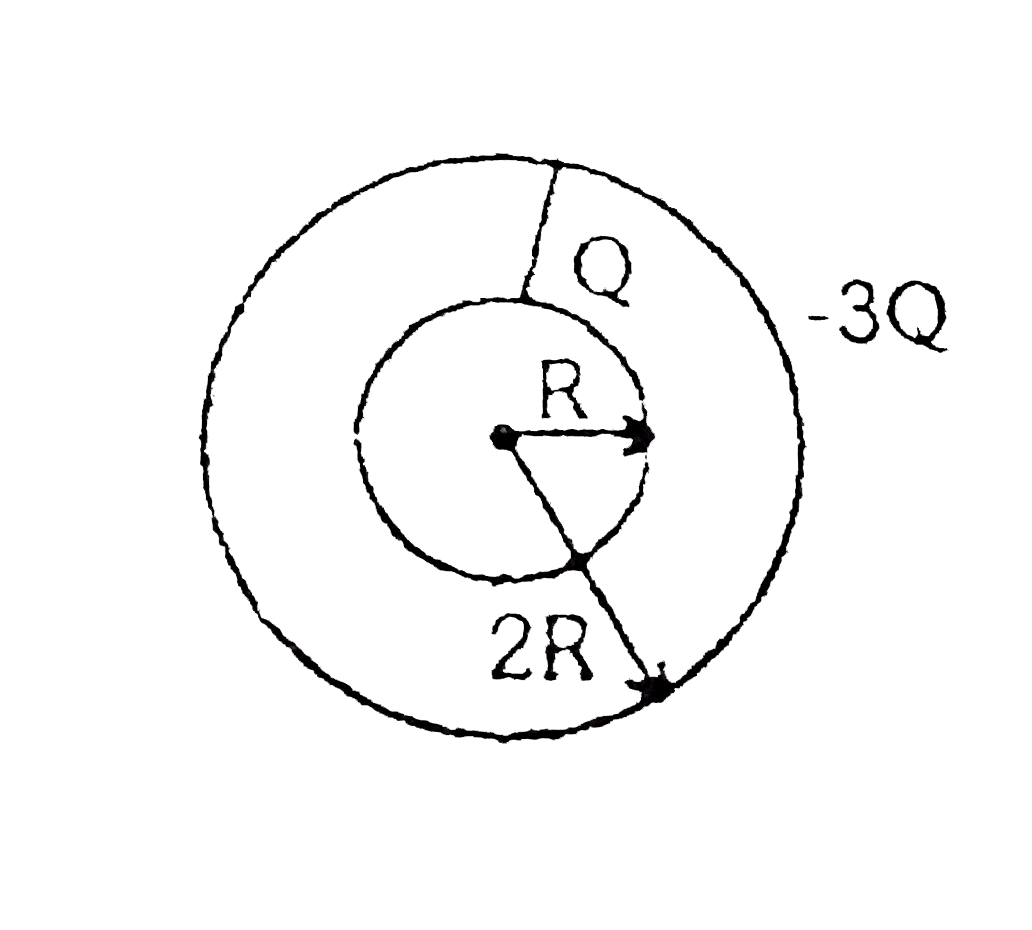
  5. Two conducting hollow spherical shells of radius R and 2R carry charge...

    Text Solution

    |

  6. An isolated conducting sphere of charge Q and radius R is connected to...

    Text Solution

    |

  7. Two positrons (e+) and two protons (p) are kept on four corners of a s...

    Text Solution

    |

  8. Four charges are placed at the circumference of a dial clock as shown ...

    Text Solution

    |

  9. A small electric dipole is placed at origin with its dipole moment dir...

    Text Solution

    |

  10. Uniform electric field of magnitude 100 V//m in space is directed alon...

    Text Solution

    |

  11. Figure shows a uniformly charged hemisphere of radius R. It has a volu...

    Text Solution

    |

  12. A metallic rod of length I rotates at angular velocity omega about an...

    Text Solution

    |

  13. Consider a finite charged rod. Electric field at point P (shown) makes...

    Text Solution

    |

  14. The alectric potential in a region is given by the relation V(x)=4+5x^...

    Text Solution

    |

  15. A thin homogeneous rod of mass m and length l is free to rotate in ver...

    Text Solution

    |

  16. A thin homogeneous rod of mass m and length l is free to rotate in ver...

    Text Solution

    |

  17. A thin homogeneous rod of mass m and length l is free to rotate in ver...

    Text Solution

    |

  18. A simple pendulum is suspended in a lift which is going up with an acc...

    Text Solution

    |

  19. The variation of potential with distance x from a fixed point is shown...

    Text Solution

    |

  20. The energy density u is plotted against the distance r from the centre...

    Text Solution

    |