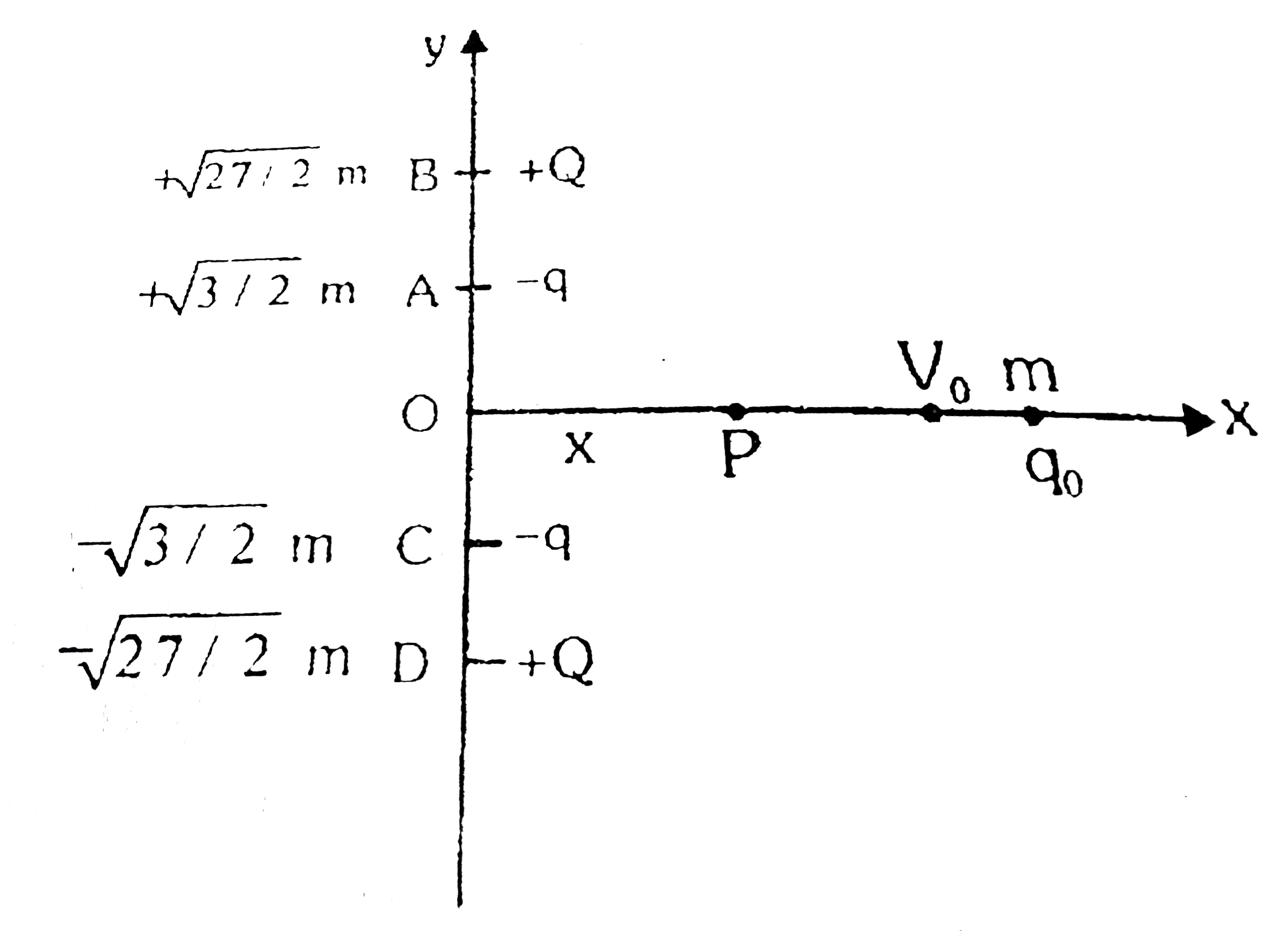Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN-MISCELLANEOUS-SUBJECTIVE QUESTION
- A conducting sphere S1 of radius r is attached to an insulating handle...
Text Solution
|
- A non-conducting disc of radius a and uniform positive surface charge ...
Text Solution
|
- Four point charges +8muC,-1muC,-1muC and , +8muC are fixed at the poin...
Text Solution
|
- A small ball if mass 2 xx 10^(-3) Kg having a charges of 1 mu C is su...
Text Solution
|
- Charges +q and -q are located at the corners of a cube of side as show...
Text Solution
|
- A charge +Q is fixed at the origin of the co-ordinate system while a s...
Text Solution
|
- There are two large parallel metallic plates S(1) and S(2) carrying su...
Text Solution
|
- A conducting liquid bubble of radius a and thickness t ( tltlt a) is ...
Text Solution
|
- A solid sphere of radius R has a charge Q distributed in its volume wi...
Text Solution
|