Home
Class 11
PHYSICS
The position time graph for two particl...

The position time graph for two particles- 1 and 2- performing SHM along X axis has been shown in the fig.
(a) Write the velocity of the two particles as a function of time.
(b) If the energy of SHM for the two particles is same write the ratio of their masses.

Text Solution

Verified by Experts

The correct Answer is:
`v_(1)=A(pi)/(t_(0))cos((pi)/(t_(0))t) " and " v_(2)=2A(pi)/(t_(0)) sin((pi)/(t_(0))t)`
`2:1`
Promotional Banner

Topper's Solved these Questions

  • SIMPLE HARMONIC MOTION

    ARIHANT|Exercise Level 2|33 Videos

  • SIMPLE HARMONIC MOTION

    ARIHANT|Exercise Level 3|9 Videos

  • ROTATIONAL MOTION

    ARIHANT|Exercise PHYSICS|159 Videos

  • SURFACE TENSION

    ARIHANT|Exercise Surface tension|33 Videos

Similar Questions

Explore conceptually related problems

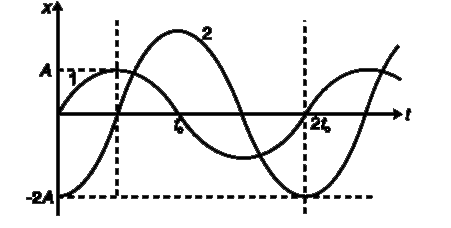
The position-time graph for two particles P and Q moving on x-axis is shown in the figure. Then

Two particles are performing SHM in same phase. It means that

The velocity versus time graph of two particles moving along x-axis varies are shown in the following two plots. Then

Velocity time graphs of particles A and B moving along x -axis are shown here. Both A and B start from origin:

displacement versus time curve for a particle executing SHM is is as shown in figure. At what points the velocity of the particle is zero?

The position time graph for a particle moving along X axis has been shown in the fig. At which of the indicated points the particle has (i) negative velocity but acceleration in positive X direction. (ii) positive velocity but acceleration in negative X direction. (iii) received a sharp blow (a large force for negligible interval of time)?

The acceleration - time graph for a particle moving along x - axis is shown in figure, If the initial velocity of particle is -5m//s , the velocity at t = 8 s is

The displacement-time graph for two particles is as shown. Find the ratio of their velocities.

The displacement - time graph of a particle executing SHM is as shown in the figure. The maximum velocity of the particle is