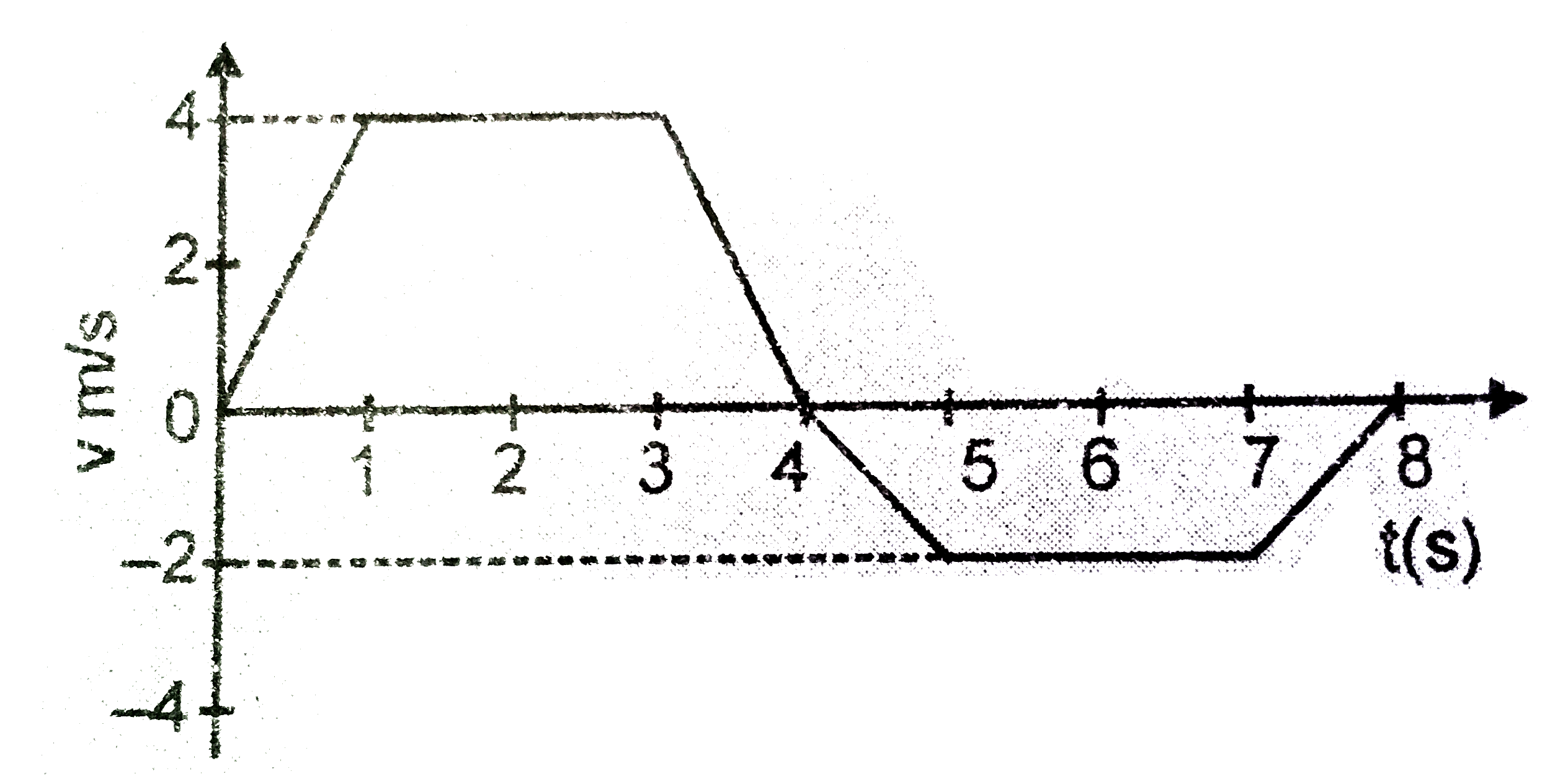
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN-KINEMATICS-Integer Type Question
- A river of width 'd' with straight parallel banks flows due North with...
Text Solution
|
- A train is moving along a straight line with a constant acceleration '...
Text Solution
|
- A rocket is moving in a gravity free space with a constant acceleratio...
Text Solution
|
- Airplanes A and B are flying with constant velocity in the same vertic...
Text Solution
|